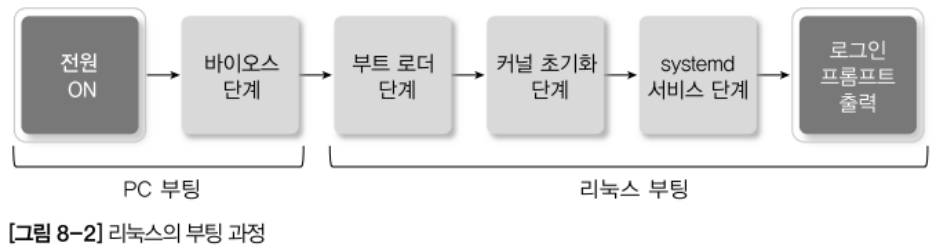
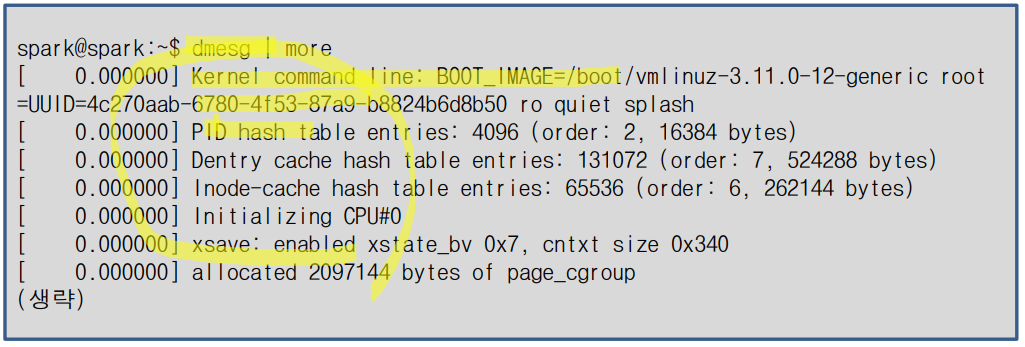
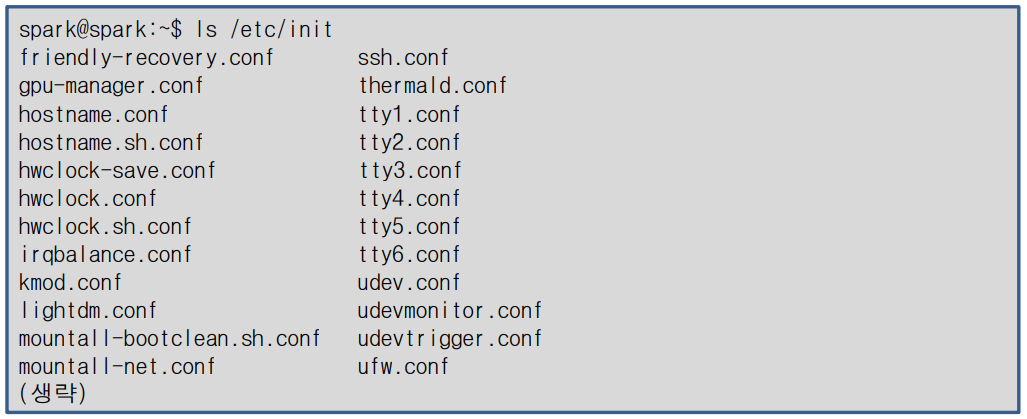
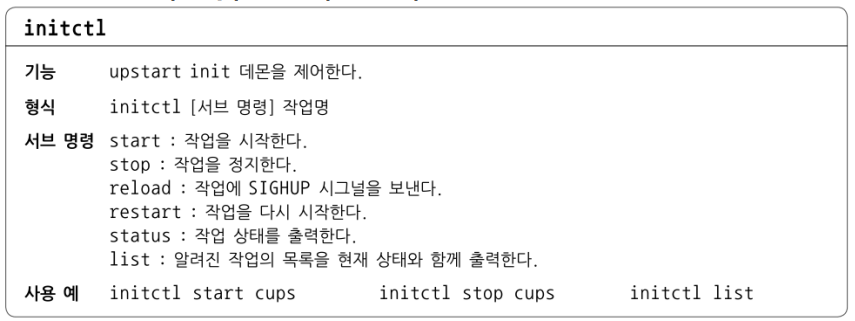
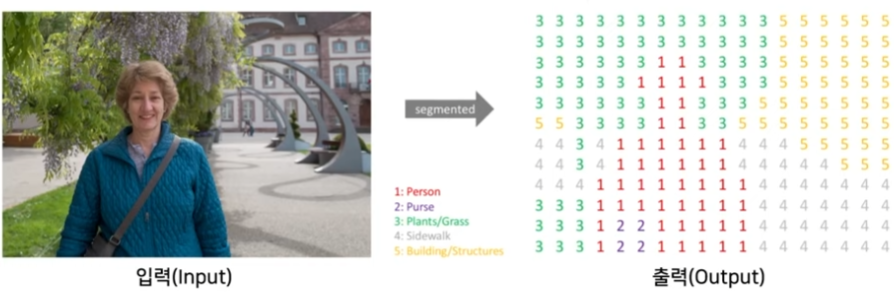
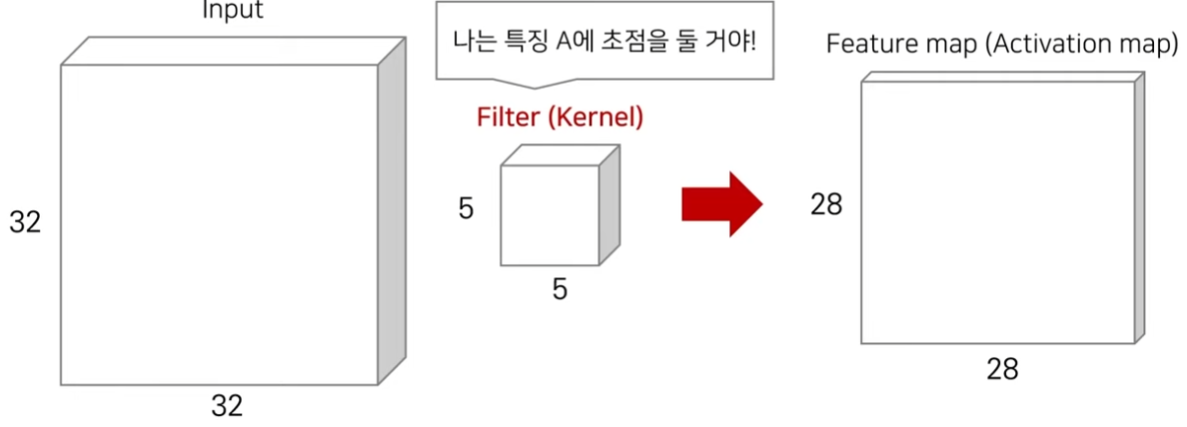
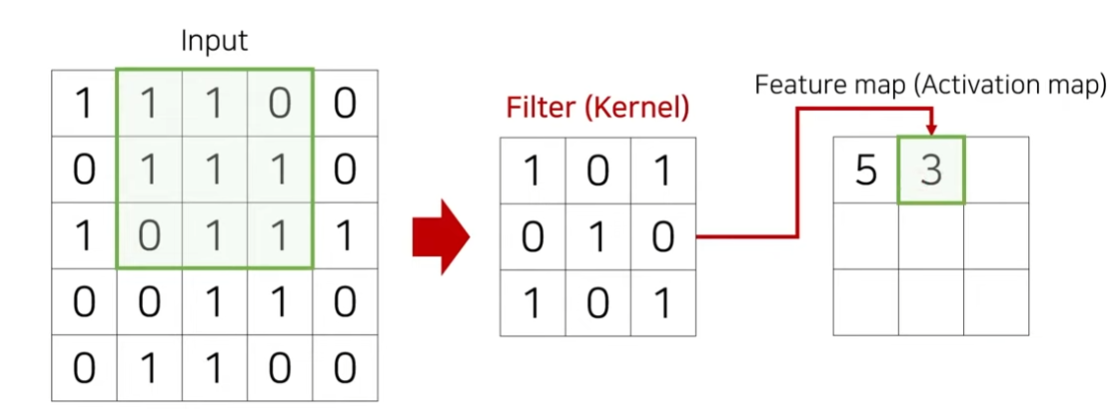
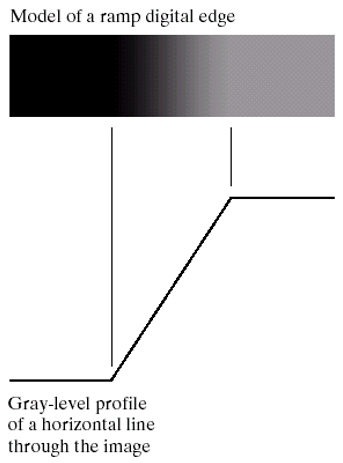
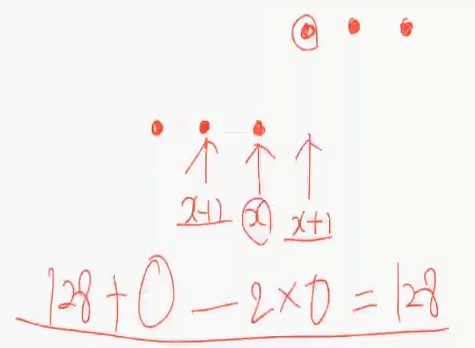
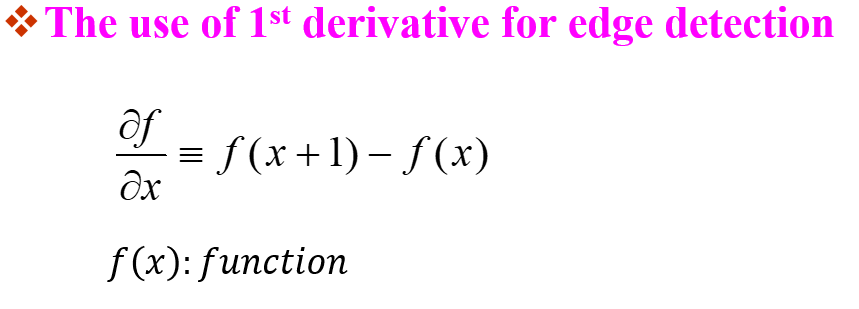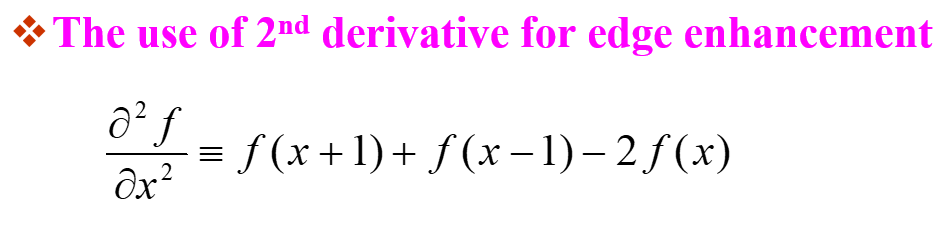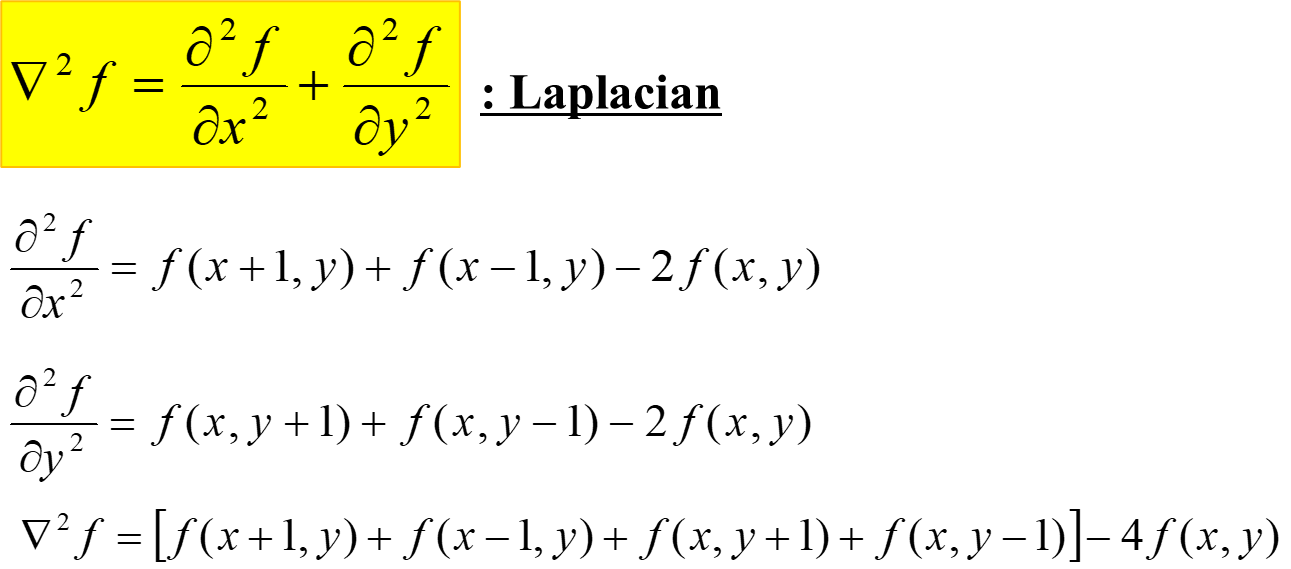거실 면적과 집 가격 사이의 선형회귀 가격정보의 관계를 측정하자.
| Living area(feet2) | Price(1000$s) |
| 2014 | 400 |
| 1600 | 330 |
| 2400 | 369 |
| 1416 | 232 |
| 3000 | 540 |
| ... | ... |
2차 평면상에 마킹이 가능하다.
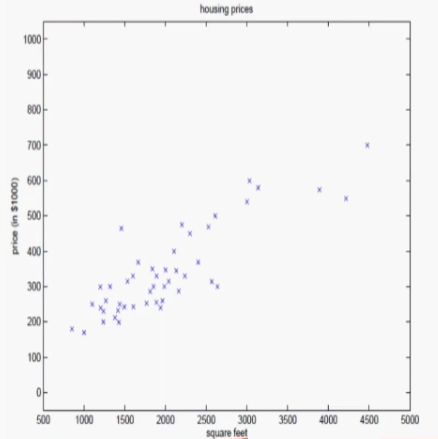
어떠한 임의의 값에 대한 출력값을 예측하는 기법 = 선형회귀
선형회귀 = 주어진 데이터로 부터 그 데이터를 가장 잘 표현할 수 있는 라인 한개를 찾는 것.
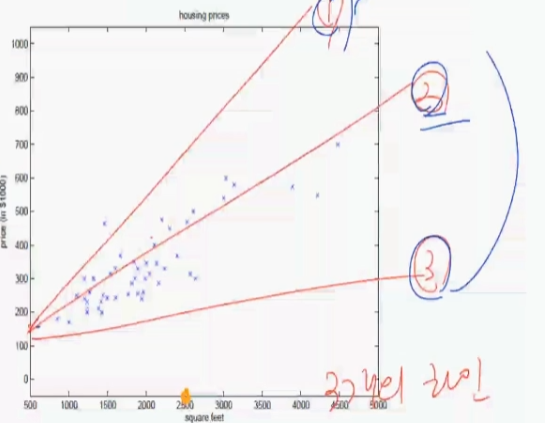
여기서 추정한 라인과 수집된 데이터 간의 오차가 크다 라면 옳은 라인이 아니다.
이런 2차원 방정식에서 직선 말고도 2차함수가 사용 될 수 있는데, 이러한 2차함수를 사용한 그래프를
Training Set : M개의 거실면적, 가격정보 쌍
y = h0(x)h0(x) : 피라미터 로 모델링 된 가설 함수
Learning algorithm : 파라미터를 추정하는 기법
선형회귀에서의 각 집의 거실 면적 및 침대 수 에 대한 가격 정보 등
각 차원 벡터와 장소, 위치, 거실면적 등의 N개의 차원벡터가 존재한다.
각 특징 벡터가 4개의 특징벡터가 생성된다.
정리하자면, 선형회귀란.
입력 벡터 (연속데이터) 에 대하여 목표값 y를 예측하는것.
목표는 각 훈련 집합에 대한 y 가 h가 되도록하는 y = h(x) 를 찾는것.
손실함수 J(0) : 추정치와 측정치의 오차를 표현한 식. 크면 안좋다.
선형회귀와 로지스틱 회귀의 차이점.
선형회귀 = Y값을 카운팅 할 수 없다. 정해져있지 않다.
로지스틱 회귀 = Y값이 정해져있는 범위를 카운팅 할 수 있다.
선형회귀 에서는 위 방식의 알고리즘을 선형방정식으로 표현한다.
선형방정식 = [
직선방정식
평면방정식
초평면 방정식 등
]
'대학교 코딩공부 > 최적화론' 카테고리의 다른 글
| 13주차 선형회귀 파라미터 추정 (0) | 2022.11.30 |
|---|---|
| 12주차 선형회귀 손실함수 (0) | 2022.11.17 |
| 최적화론 10주차 (분류기 구현 단계) (0) | 2022.11.05 |
| 최적화론 9주차 특징 추출 (0) | 2022.10.26 |
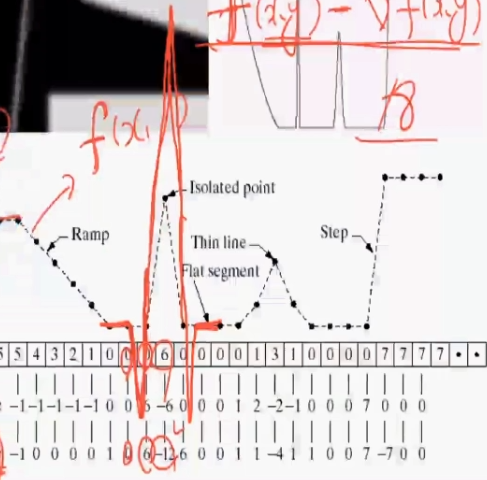
| 최적화론 2주차 도함수 [ 미분계수 응용 ] (0) | 2022.09.06 |