도함수 = 미분 이라고 해도 무방하다.
접선 문제
곡선의 접선은 그 곡선에 접하는 직선을 의미한다.
접선 = 접하는 선. 다른선과 접하는 선을 이야기한다.

위 이미지에서 점 P 는 (x,y) = (1,1) 위 그림에서의 접선은 P 지점에 접하는 선 을 의미함.
y=x^2의 곡선에 접해있는 점 P에 접하는 접선을 구하라. 접선의 방정식은 어찌되나?
이때 접선 = 직선이다. 직선의 방정식으로 표현이 가능하다.
원점을 지나는 임의의 직선 = y=ax라고 표현 가능하다.
원점을 지나지 않는 임의의 직선 = y=ax+b라고 표현이 가능하다. 이떄, a = 기울기 b = y절편 이라고 이야기한다. [ y를 지나는 선 의 위치 ]
임의의 직선의 위치 = y = ax + b라고 이야기한다. 이때, P(1,1)을 지나야 하기 때문에, y-y1 = a(x-x1) 라고 나타낸다.
위 이미지를 y1 과 x1에 대입하면 y-1 = a(x-1) 이라고 한다. 이때 a값은 기울기이다. 위 방정식 대로 대입하면 식은 나오지만, 기울기는 알 수 없기 때문에 기울기를 알아야 한다.

P점을 알고 있음으로 그 외에 y=x^2 의 곡선 내부의 임의의점을 지정해서 직선을 만든다.
할선 = 임의의 점을 지정해서 만든 직선
이때 할선의 기울기는 우리가 계산 할 수 있다. P점과 임의의 Q점의 위치값을 이용하여 기울기를 알 수 있다.
이후 Q위치를 P지점으로 천천히 이동시킨다고 가정한다.
 |
 |
위 이미지는 그전 이미지보다 T와의 각도차이가 크게 나지 않는 점을 알 수 있다. 그렇게 계속해서 이동시키면
P와 Q가 위치가 거의 동일해지면 T의 접선과 거의 동일한 모양이 된다는 사실을 알 수 있다.
반대로 왼쪽부터 임의의 Q를 지정하여 가깝게 다가간다고 하더라도 동일한 결과를 얻을 수 있다.
Q지점의 x좌표 = x y좌표 =x^2 이 된다.Q=(x,x^2)
이때 기울기를 구하는 방식은 = x증가량 분의 y증가량. x= x-1 y=x^2-1 즉,
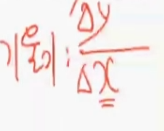 |
 |
점 P의 위치인 1에서 x까지 변한값. 점 P의 Y위치는 1 에서 x^2까지 변했기 때문에 위의 공식이 성립된다.
lim 밑의 x->1 의 의미는 x값을 1로 바꾸어 갔을 때, [ 극한할때 ]
극한 = x값이 1에 가까이 가면 lim옆의 값이 어떠한 값으로 변해간다 라는 뜻. 그리고 그러한 값이 여기서 구하려고 하는 기울기와 같다.
m은 기울기 임으로 x가 1로 가까이 갈 수록 m이 되어간다 라고 할 수 있다.
그러므로 최종값은 기울기가 극한이면 m=2에 도달한다.
결과로는 y-y1 = m(x-x1) 임으로, x가 1에 극한했을 때 기울기가 2 임으로, y-1 = 2(x-1)이 된다.
다시 정리하면 y = 2x-1이 된다는 결과가 나온다!
결국 그러한 곡선위의 한 점에서 그 곡선에 대한 접선의 기울기를 가리켜 그 점에서의 곡선의 기울기 라 부른다!
여기서 Q값의 x를 4로 지정하면 y=x^2임으로 Q(4,16) 이고 (16-1)/(4-1) 임으로 5이다. x->1임으로 1과차이가 남으로 x가 4일때의 기울기는 5라고 할 수 있다. x값을 더 내려서 3으로 옮기고 2로 옮기면서 x와 비슷한 값에극한되게 노가다를 한다.
x가 2일경우 y는 4임으로 Q(2,4), (4-1)/(2-1) = 3 x가 2일때 a=3이다. 즉, x가 1에 가까워질 수록 4->3->1 로 가까워 진다는것을 알 수 있다.
다른 예제로 살펴보면,
 |
 |
PQ의 기울기를 계산하면,
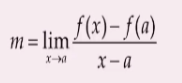
이때 x-a를 h로 바꿔서 공식을 재배열해보면,
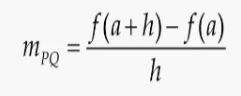
즉, x가 a에 가까워지는게 x->a가 되는데, h=x-a임으로 h=0에 가까워진다고 볼 수 있다.
x-a가 x의 증가량을 의미하는 델타 x임으로 h=x증가량이라고 할 수 있다.
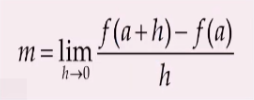
점(3,1)에서 쌍곡선 y=3/x의 접선의 방정식을 구하라.
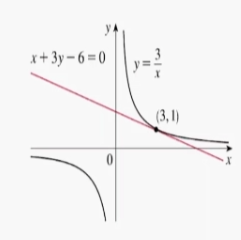
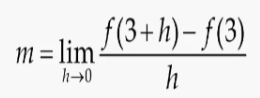
이때 f(x) = 3/x임으로, 대입하여 계산하면,
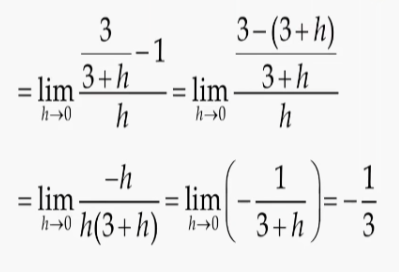
위와 같이 계산공식이 나온다. 수식상 h = 0으로 극한함으로 h=0으로 함으로 기울기는 -1/3임을 알 수 있다.
한점을 지나는 접선의 방정식 = y-y1 = m(x-x1) 이기 때문에, 기울기가 -1/3임을 알게 되었음으로,
y-1 = -1/3(x-3)으로 표현할 수 있다. 즉, x+3y-6 = 0 이라고 나오게 된다.!
미분 계수 = 접선의 기울기
f' = 미분계수 라고 말함.

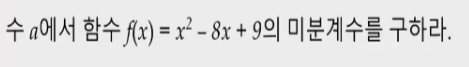
f(x) = x^2-8x +9 임으로
lim[x->a] = (x^2-8x+9) - f(a)
lim[h->0] = ([(a+h)^2 -8(a+h) + 9] - (a^2 - 8a + 9)) / h
=(a^2 + 2ah + h^2 - 8a - 8h + 9 - a^2 +8a -9) /h
=(2ah +h^2 - 8h) /h
=2a + h - 8
이때 h는 극한으로 0이 됨으로 0을 대입.
=2a-8
f'(a) = 2a-8
'대학교 코딩공부 > 최적화론' 카테고리의 다른 글
| 12주차 선형회귀 손실함수 (0) | 2022.11.17 |
|---|---|
| 11주차 Linear & Logistic Regression ( 선형 회귀 ) (0) | 2022.11.13 |
| 최적화론 10주차 (분류기 구현 단계) (0) | 2022.11.05 |
| 최적화론 9주차 특징 추출 (0) | 2022.10.26 |
| 최적화론 2주차 도함수 [ 미분계수 응용 ] (0) | 2022.09.06 |
