머신러닝의 프로세스는 다음 3가지 과정을 거친다.
- 학습하고자 하는 가설(Hypothesis) h(세타)을 수학적 표현식으로 표현
- 가설의 성능을 측정할 수 있는 손실함수(LossFunction) J(세타)을 정의한다.
- 손실함수 J(세타)를 최소화(Minimize)할 수 있는 학습 알고리즘을 설계한다.
선형 회귀 모델에 대입하여 생각하면 다음과 같다.
선형 회귀 모델은 선형 함수를 이용해서 회귀를 수행하는 기법.
다음 가설로 표현한다.
y=Wx+b
이 때 x 와 y는 데이터로부터 주어지는 인풋데이터, 타겟데이터 이고 W와 b는 파라미터 세타 라고 부르며, 트레이닝데이터 로부터 학습을 통해 적절한 값을 내야하는값.
손실함수
여러가지 형태로 정의될 수 있지만, 그중 가장 대표적인 손실 함수 중 하나는 평균 제곱 오차이다.
MSE는 다음 수식으로 나타낸다.
MSE=12n∑i=1n(ˆyi−ˆyi)2
예를들어 정답이 y = [1, 10, 13, 7] 이고,
모델이 y = [10, 3, 1, 4] 와 같이 잘못된 값을 예측하면
MSE 손실 함수는 35.375라는 큰 값을 도출한다.
MSE=12∗4((10−1)2+(3−10)2+(1−13)2+(4−7)2)=1.5
하지만, 예측값이 [ 2, 10, 11, 6 ] 와 같이 유사하다면, 손실함수는 다음과 같은 결과가 나타난다.
MSE=12∗4((2−1)2+(10−10)2+(11−13)2+(6−7)2)=1.5
손실함수는 목적에 가까운 형태로 파라미터가 최적화되었을 때, 더 작은 값을 갖는 특성을 가져야 한다.
이러한 손실함수를 다른말로 비용 함수 라고 부른다.
그냥 임의의 함수로, 오차가 나타난다는걸 표현할 수 있는 수식이면 전부다 손실함수로 기용할 수는 있기는 하다.
선형회귀 직접 구현작업 해보기
import tensorflow as tf
import matplotlib.pyplot as plt
# 선형회귀 모델 (Wx + b)을 위한 tf.Variable을 선언
W = tf.Variable(tf.random.normal(shape=[1]))
b = tf.Variable(tf.random.normal(shape=[1]))
# 가설 정의 함수 생성
@tf.function
def linear_model(x):
return W * x + b
# 손실 함수 정의
# MSE 손실 함수 \mean{(y' - y)^2}
@tf.function
def mse_loss(y_pred, y):
return tf.reduce_mean(tf.square(y_pred - y))
# 최적화를 위한 그라디언트 디센트 옵티마이저를 정의
optimizer = tf.optimizers.SGD(0.01) # 가장 기본적인 옵티마이저
# 최적화를 위한 function을 정의
@tf.function
def train_step(x, y):
with tf.GradientTape() as tape:
y_pred = linear_model(x)
loss = mse_loss(y_pred, y)
gradients = tape.gradient(loss, [W, b])
optimizer.apply_gradients(zip(gradients, [W, b]))
# 트레이닝을 위한 입력값과 출력값을 준비
x_train = [1, 2, 3, 4] # 인풋으로 1, 2, 3, 4 를 넣으면
y_train = [2, 4, 6, 8] # 아웃풋 으로 2, 4, 6, 8 이 나와야 한다.
# numpy array로 변환
x_train = tf.constant(x_train, dtype=tf.float32)
y_train = tf.constant(y_train, dtype=tf.float32)
# 학습 과정 실행
for i in range(1000):
train_step(x_train, y_train)
# 테스트 입력값 준비
x_text = [3.5, 5, 5.5, 6]
# 테스트 데이터를 이용해 학습된 선형회귀 모델이 데이터의 경향성 (y = 2x)인지
# 확인
# 학습 후 결과 출력
print(linear_model(x_text).numpy())
# 예상참값. [7, 10, 11, 12]
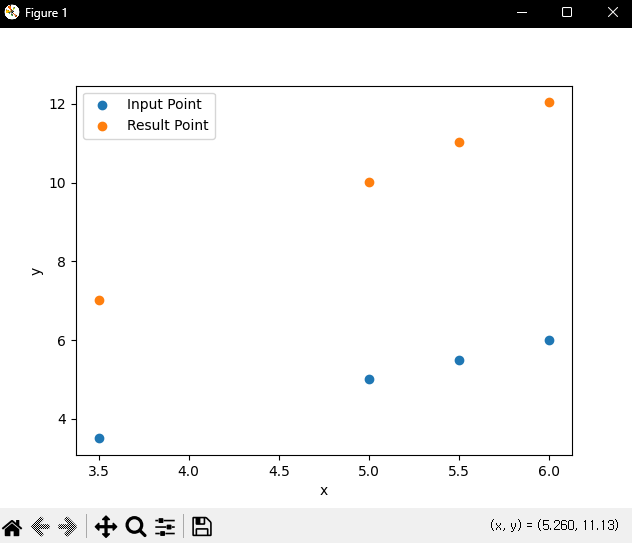
# 학습된 모델 시각화
plt.scatter(x_text, x_text, label='Input Point')
plt.scatter(x_text, linear_model(x_text).numpy(), label='Result Point')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
Visual Code로 구현하여 작업한다.
우리가 찾으려는 값은 W, b이다.
y = W * x + b 라는 수식이기 때문에, 아직 정의되어있지 않은 W와 b를 찾아가는 과정.
랜덤한 임의의 W와 b로 값을 도출하고, 도출된 결과값에 loss값을 확인, loss에 따라 W와 b를 재조정 한 후 다시 반복한다.
이걸 for문으로 1000번 반복하여 결과를 수렴시키면 원하는 W와 b값이 나타나게 된다.
그리고 이 결과가 제곱승이 되는것.
물론, 직접 구현할수는 있다. 선형회귀 임으로, 수식값에 W와 b에 수렴하도록 수식을 수정하면 된다. 값의 고저차에 따른 수정값은 약 0.01이나 0.1정도로 넣는편.
'알고리즘' 카테고리의 다른 글
| Overfitting 과 Underfitting (0) | 2024.06.13 |
|---|---|
| Batch Gradient Desent, Stochastic Gradient Descent, Mini-Batch Gradient Desent (1) | 2024.06.13 |
| Q & Optimal Policy (1) | 2024.06.09 |
| MDP ( Markov Decision Process ) (1) | 2024.06.09 |
| Greedy Action으로 알아보는 Q-Learning (0) | 2024.06.07 |
