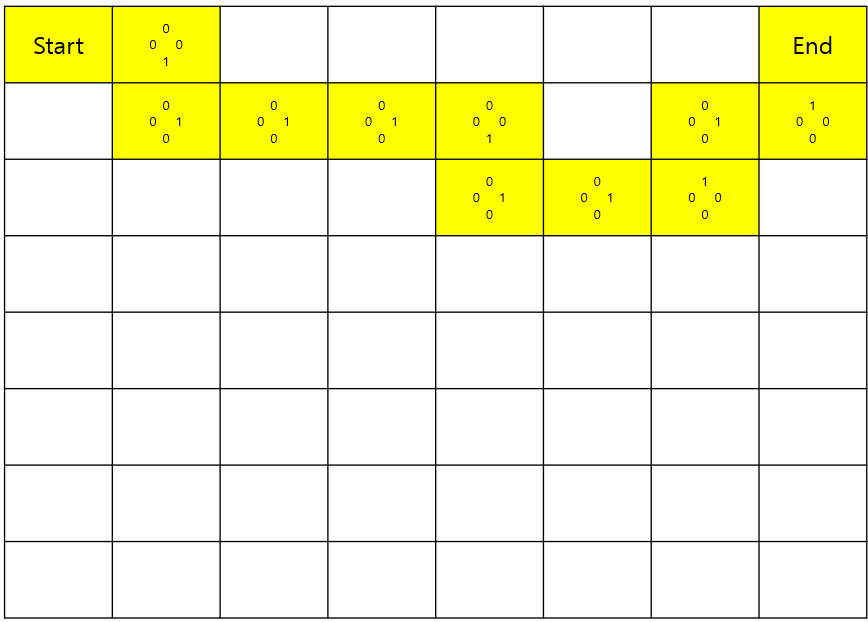
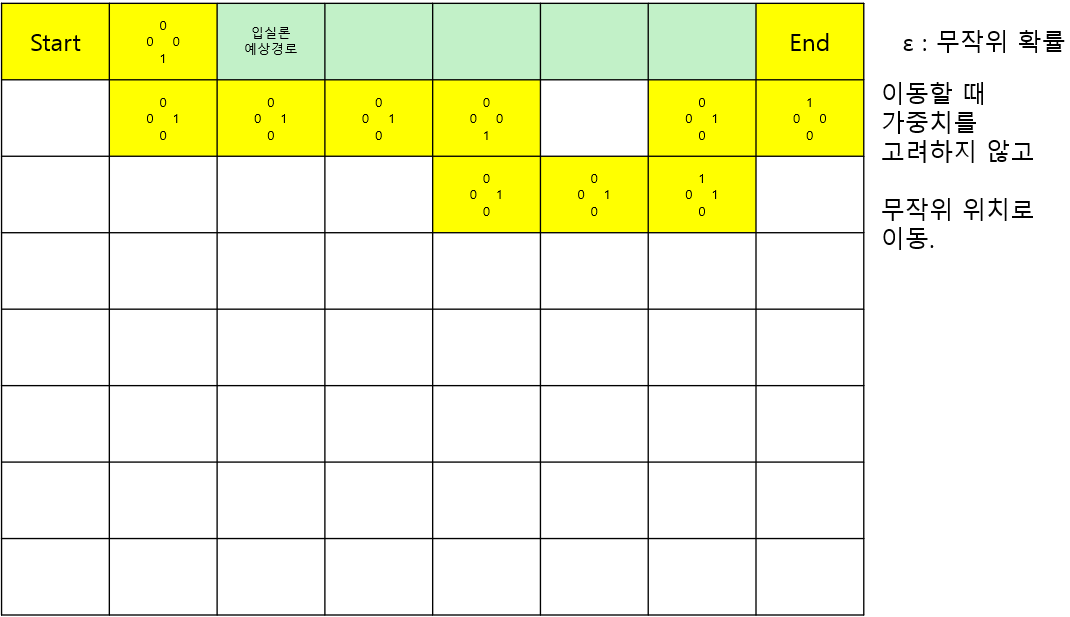
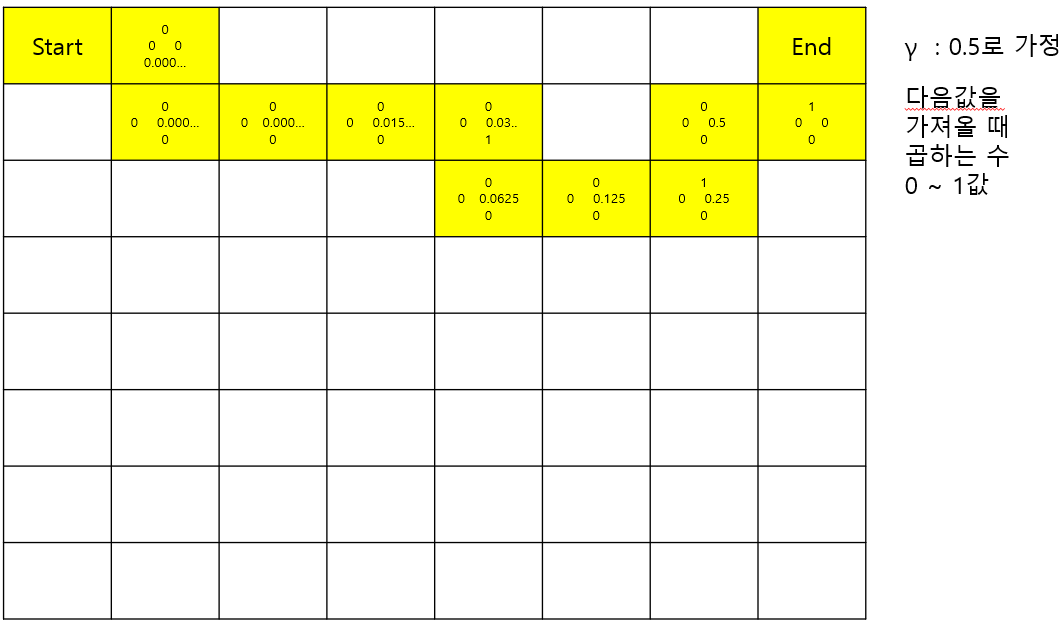
그레디언트 수식 계산방식들로 2가지에, 2가지의 장단점을 합친 한가지를 말할 수 있다.

Batch Gradient Descent

경사하강법의 한 스텝 업데이트 시 전체 트레이닝 데이터를 하나의 Batch로 만들어 사용하기 때문에 Batch Gradient Descent라고 부른다.

그레디언트 수식을 계산할 때, 100만개 이상의 매우 많은 손실함수 미분값을 전부 더한 뒤 평균을 취해서 파라미터를 업데이트 하게 되면 매우 큰 연산량 낭비가 일어난다.

한 스텝을 연산하는데 많은 시간이 걸리게 되고, 결과적으로 최적의 파라미터를 찾는데 오랜 시간이 걸린다.

옵티마이저 시간이 매우 길어지게 된다.

한 스텝 업데이트를 위해 계산하는 손실함수의 미분값은 아래 수식으로 나타낸다.

$  \frac{\partial }{\partial \partial _{1}}J( \theta _{0},\theta _{1}) = \frac{\partial }{\partial \partial _{1}}\frac{1}{2n}\sum_{i=1}^{n}(\hat{y_{i}} - y_{i})^{2} $

$  \frac{\partial }{\partial \partial _{0}}J( \theta _{0},\theta _{1}) = \frac{\partial }{\partial \partial _{0}}\frac{1}{2n}\sum_{i=1}^{n}(\hat{y_{i}} - y_{i})^{2} $

그에대한 반대적인 개념으로 경사하강법의 한 스텝 업데이트마다 1개의 트레이닝 데이터만 사용하는 기법을 

Stochastic Gradient Descent 기법 이라고 한다.

Stochastic Gradient Descent

Stochastic Gradient Descent  기법 을 사용하면 파라미터를 자주 업데이트 할 수 있지만,

한번업데이트 할 때 전체 트레이닝 데이터의 특성을 고려하지 않고 각각의 트레이닝 데이터의 특성만을 고려하므로 부정확한 업데이트가 진행될 수 있다.

$  \frac{\partial }{\partial \partial _{0}}J( \theta _{0},\theta _{1}) = \frac{\partial }{\partial \partial _{0}}(\hat{y} - y)^{2} $

$  \frac{\partial }{\partial \partial _{1}}J( \theta _{0},\theta _{1}) = \frac{\partial }{\partial \partial _{1}}(\hat{y} - y)^{2} $

그리하여 실제 문제를 해결할 때 에는 두개의 절충 기법인 Mini-Batch Gradient Desent를 많이 이용한다.

Mini-Batch Gradient Desent는, 전체 트레이닝 데이터 Batch가 1000(n)개라면 이를 100(m)개씩 묶은 Mini-Batch개수만큼의 손실 함수 미분값 평균을 이용해서 파라미터를 한 스텝을 업데이트하는 기법이다.

Mini-Batch Gradient Desent 기법에서 한 스텝 업데이트를 위해 계산하는 손실 함수의 미분값은 아래 수식으로 나타낼 수 있다.

$  \frac{\partial }{\partial \partial _{0}}J( \theta _{0},\theta _{1}) = \frac{\partial }{\partial \partial _{0}}\frac{1}{2m}\sum_{i=1}^{m}(\hat{y_{i}} - y_{i})^{2} $

$  \frac{\partial }{\partial \partial _{1}}J( \theta _{0},\theta _{1}) = \frac{\partial }{\partial \partial _{1}}\frac{1}{2m}\sum_{i=1}^{m}(\hat{y_{i}} - y_{i})^{2} $

머신러닝의 프로세스는 다음 3가지 과정을 거친다.

1. 학습하고자 하는 가설(Hypothesis) h(세타)을 수학적 표현식으로 표현
2. 가설의 성능을 측정할 수 있는 손실함수(LossFunction) J(세타)을 정의한다.
3. 손실함수 J(세타)를 최소화(Minimize)할 수 있는 학습 알고리즘을 설계한다.

선형 회귀 모델에 대입하여 생각하면 다음과 같다.

선형 회귀 모델은 선형 함수를 이용해서 회귀를 수행하는 기법.

다음 가설로 표현한다.

$ y = Wx + b $

이 때 x 와 y는 데이터로부터 주어지는 인풋데이터, 타겟데이터 이고 W와 b는 파라미터 세타 라고 부르며, 트레이닝데이터 로부터 학습을 통해 적절한 값을 내야하는값.

손실함수

여러가지 형태로 정의될 수 있지만, 그중 가장 대표적인 손실 함수 중 하나는 평균 제곱 오차이다.

MSE는 다음 수식으로 나타낸다.

$ MSE = \frac{1}{2n}\sum_{n}^{i=1}(\hat{y}_{i}-\hat{y}_{i})^{2} $

예를들어 정답이 y = [1, 10, 13, 7] 이고,

모델이 y = [10, 3, 1, 4] 와 같이 잘못된 값을 예측하면

MSE 손실 함수는 35.375라는 큰 값을 도출한다.

$ MSE = \frac{1}{2 * 4}{((10 - 1)^{2} + (3 - 10)^{2} + (1 - 13)^{2} + (4 - 7)^{2})} = 1.5 $

하지만, 예측값이 [ 2, 10, 11, 6 ] 와 같이 유사하다면, 손실함수는 다음과 같은 결과가 나타난다.

$ MSE = \frac{1}{2 * 4}{((2 - 1)^{2} + (10 - 10)^{2} + (11 - 13)^{2} + (6 - 7)^{2})} = 1.5 $

손실함수는 목적에 가까운 형태로 파라미터가 최적화되었을 때, 더 작은 값을 갖는 특성을 가져야 한다.

이러한 손실함수를 다른말로 비용 함수 라고 부른다.

그냥 임의의 함수로, 오차가 나타난다는걸 표현할 수 있는 수식이면 전부다 손실함수로 기용할 수는 있기는 하다.

선형회귀 직접 구현작업 해보기

import tensorflow as tf
import matplotlib.pyplot as plt

# 선형회귀 모델 (Wx + b)을 위한 tf.Variable을 선언
W = tf.Variable(tf.random.normal(shape=[1]))
b = tf.Variable(tf.random.normal(shape=[1]))

# 가설 정의 함수 생성
@tf.function
def linear_model(x):
    return W * x + b

# 손실 함수 정의
# MSE 손실 함수 \mean{(y' - y)^2}
@tf.function
def mse_loss(y_pred, y):
    return tf.reduce_mean(tf.square(y_pred - y))

# 최적화를 위한 그라디언트 디센트 옵티마이저를 정의
optimizer = tf.optimizers.SGD(0.01) # 가장 기본적인 옵티마이저

# 최적화를 위한 function을 정의
@tf.function
def train_step(x, y):
    with tf.GradientTape() as tape:
        y_pred = linear_model(x)
        loss = mse_loss(y_pred, y)
    gradients = tape.gradient(loss, [W, b])
    optimizer.apply_gradients(zip(gradients, [W, b]))

# 트레이닝을 위한 입력값과 출력값을 준비
x_train = [1, 2, 3, 4]  # 인풋으로 1, 2, 3, 4 를 넣으면
y_train = [2, 4, 6, 8]  # 아웃풋 으로 2, 4, 6, 8 이 나와야 한다.

# numpy array로 변환
x_train = tf.constant(x_train, dtype=tf.float32)
y_train = tf.constant(y_train, dtype=tf.float32)

# 학습 과정 실행
for i in range(1000):
    train_step(x_train, y_train)

# 테스트 입력값 준비
x_text = [3.5, 5, 5.5, 6]

# 테스트 데이터를 이용해 학습된 선형회귀 모델이 데이터의 경향성 (y = 2x)인지 
# 확인

# 학습 후 결과 출력
print(linear_model(x_text).numpy())
# 예상참값. [7, 10, 11, 12]

# 학습된 모델 시각화
plt.scatter(x_text, x_text, label='Input Point')
plt.scatter(x_text, linear_model(x_text).numpy(), label='Result Point')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

Visual Code로 구현하여 작업한다.

우리가 찾으려는 값은 W, b이다.

y = W * x + b 라는 수식이기 때문에, 아직 정의되어있지 않은 W와 b를 찾아가는 과정.

랜덤한 임의의 W와 b로 값을 도출하고, 도출된 결과값에 loss값을 확인, loss에 따라 W와 b를 재조정 한 후 다시 반복한다.

이걸 for문으로 1000번 반복하여 결과를 수렴시키면 원하는 W와 b값이 나타나게 된다.

그리고 이 결과가 제곱승이 되는것.

물론, 직접 구현할수는 있다. 선형회귀 임으로, 수식값에 W와 b에 수렴하도록 수식을 수정하면 된다. 값의 고저차에 따른 수정값은 약 0.01이나 0.1정도로 넣는편.

ImageAiCon PP

진행중인 작업

프리뷰 로드아웃 제작중

알고리즘 학습중...

https://inradestrt.tistory.com/656

https://inradestrt.tistory.com/657

진행 예정 작업
(예상)

1. Unreal의 ImageAI공부하기
   
   1. CNN알고리즘 다시 복기하기
   2. 알고리즘 선별( 현 예상안 으로는,DQN알고리즘 사용예정)
   3. 알고리즘 관련 강의 학습( 자본이 준비되면 강의학습을 진행하며 정리사항 정리예정)
2. Unreal ImageRetargeting 코드제작
   1. 언리얼 함수 상으로 지정된 카메라의 타겟뷰를 이미지값으로 저장 반환하는 방식이 존재함.
   2. TCP방식으로 데이터 통신처리를 진행
   3. TensorFlow를 사용하여 전달받은 이미지로 학습 알고리즘 연산.
   4. 연산결과를 다시 언리얼로 전달하여 학습된 데이터를 갱신.
   5. 4번과 3번을 반복
3. 학습결과확인 후 재학습
4.  5와 6을 원하는 AI행동패턴이 나타날때까지 반복

목표

1. TensorFlow를 사용하여 알고리즘이 동작하는지 직접적인 확인을 진행.
2. TensorFlow 를 사용하지 않고, 스스로의 C++코드로 알고리즘 함수 구현부를 직접 제작하여 사용하는것
   (파이썬만으로 k means clustering를 구현하였을 때, 구현객체가 C++의 연산처리속도를 따라잡지 못하는 상황이 있었음)
3. UI관련 제작방식은 C#으로, 함수부는 DLL파일로 포팅하여 언리얼 엔진에 집어넣기.

완료된 작업

Optimal Policy

최적정책이라는 말로, 행동을 더 효과적으로 가장 최선의 결과를 내도록 하는 알고리즘 이라고 생각하면 된다.

이러한 최적정책은 다양한 알고리즘이 존재하지만, 이러한 최적정책을 판별하는 도구로, 상태 가치함수와 행동 가치함수가 있다.

즉, 지금으로부터 기대되는 Return을 최대화 시키는것

과거에서는 지금까지 잘했다 치고 지금부터 미래를 본다고 이해하면 된다.

Return Gt = Rt + 감마 * Rt+1 + 감마^2 * Rt+2...

모든 가능한 경우의 수를 전부 더해서 평균내보는것.

$ E\left [f(x)  \right ] = \int f(x)P(x)dx $

가치함수

가치함수는 상태 가치함수, 행동 가치함수 두가지로 나뉜다.

각각 우선하는 사항이 다르며, 이는 다음과 같다.

State Value Function

지금부터 기대되는 Return

현재 상태에 대한 평가를 내리는것

특정 상태의 가치를 평가한다.

임의의 상태값에 따른 모든 행동을 고려하였을 때, 기대할 수 있는 모든 총 보상의 현재가치 를 의미한다.

$ V(s_{t}) _{=}^{\triangle} \int _{a_{t}:a_{\infty }}G_{t}P(a_{t},S_{t+1},a_{t+1}\cdots |S_{t})da_{t}:a_{\infty} $

가능한 스테이트 에서 전부 접근을 해보았을 때 나오는 현재 상태에서 기대되는 리턴.

Action Value Funtion

지금 행동으로부터 기대되는 Return

특정 상태에서 특정 행동의 가치를 평가한다.

임의의 특정 행동을 선택한 후, 그 행동이 주는 즉각적 보상과 이후 상태에 대해 정책을 따랐을 때 기대할 수 있는 총 보상의 현재 가치를 의미한다.

Action Value Funtion

$ Q(s_{t}, a_{t})_{=}^{\triangle }\int_{S_{t+1} : a_{\infty }}G_{t}P(S_{t+1},a_{t+1},S_{t+2},a_{t+2},\cdots|S_{t},a_{t})dS_{t+1}:a_{\infty } $

임의의 액션을 선택했을 때, 주어진 정책상 기대할 수 있는 전체보상의 현재가치.

위와같이 상태값을 판단해서 Maximize하는것이 Optimal Policy이다,

Markov Decision Process

의사결정 문제를 수학적으로 모델링 하는 방법이다.

특정 환경에서 에이전트가 어떻게 행동해야 하는지를 결정하기 위해 사용되는 방법으로. 임의의 수학공식 이라기 보다는 이러한 방법론 이 있다 정도로 받아드리면 된다.

환경의 현재 상태와 미래 상태간의 전이 가능성을 고려하여 최적의 결정을 내리는데 사용된다.

연속적으로 현재 가치에 따라 의사를 결정하는 방식이다.

여러개의 Action을 연속적으로 수행하여 S0의 동작 a0이 있고, 결과가 S1, S1의 동작이 a1 이라고 한다면,

S1에는 S0 -> a0의 상태0과 행동0을 포함한다고 볼 수 있다.

이러한 과정을 반복하여 결과를 뽑아내는것을 MDP방식 이라고 한다.

요소

상태(State) S

• 시스템의 현재 상황, 상태를 말한다.
• 에이전트의 위치, 시뮬레이션중인 상황의 현재 판도 등.

행동(Action) A

• 에이전트가 취할 수 있는 선택지 를 말한다.
• 에이전트의 이동 방향, 시뮬레이션의 다음 수

전이 확률 (Transition Probability) P

• 특정 상태에서 특정 행동을 취했을 때 다음 상태로 전이될 확률을 말한다.
• 에이전트가 오른쪽 으로 이동했을 때 다음 임의의 위치로 이동할 확률

보상 (Reward) R

의 크게 4가지 요소로 정리할 수 있다.

표현

MDP는 보통 (S, A, P, R)로 표현된다.

예시

 $ P(s^{'}|s,a) $

• 상태 s에서 행동 a를 했을 때 상태  $ s^{'} $ 로 전이될 확률

 $ R(s,a,s_{'}) $

• 상태 s에서 행동 a를 해서 상태 $ s^{'} $ 로 전이될 때 얻는 보상

정책 ( Policy )

각 상태에서 어떤 행동을 취할지를 결정하는 전략이다.

이것은 확률일수도 있고 결정일수도 있다. 정책은 보통 $ \pi (a|s) $ 로 표현된다.

상태 s에서 행동 a를 선택할 확률을 의미한다.

파이가 쓰이는이유는 딱히 없다; 그냥 파이라고 쓰고 정책이라고 읽자.

가치함수 (Value Function)

가치함수는 특정 정책을 따를 때 얻을것 으로 기대되는 보상의 총 합이다.

배가고플때 밥을 먹으러 식당으로 걸어가거나, 부엌으로 간다고 생각해보자.

밥을 먹는다 가 원하는 결과이고, 우리는 밥을 먹으러 가는 과정 자체가 보상가중치가 더해진다고 볼 수 있다.

이때, 식당을 가는행동이 나타나면 부엌에서 직접 밥을 해먹는것 보다 식당에서 먹는게더 맛있다고 여기기 때문에 식당의 가중치가 더 크다고 볼 수 있고,

부엌으로 간다면 부엌에서 해먹는 음식이 식당보다 맛있거나 임의의 다른 경재적 이득을 본다고 볼 수 있다.

이러한 결과를 유도하기 위해 보상을 주는방식이 가치함수 이다.

이는 두가지로 나눌 수 있다.

상태 가치 함수 ( State Value Function )

• 특정 상태에서 시작하여 정책을 따를 떄 얻는 기대보상을 말한다.
• $ V^{\pi}(s) $ 로 표현된다.

행동 가치 함수 ( Action Value Function )

• 특정 상태에서 특정 행동을 취하고 그 이후 정책을 따를 때 얻을 수 있는 기대보상을 말한다.
• $ Q^{\pi}(s,a) $ 로 표현된다.

벨만 방정식 ( Bellman Equation )

MDP에서 최적의 정책을 찾기위한 기본 도구이다. 함수나 수식이라고 표현하기는 하지만,

함수라고 볼수도 있지만, 이해하기 쉽게 생각하자면 가이드라인 이라고 생각하자.

상태 가치 함수:

$ V^{\pi}(s) = \sum_{a} \pi(a|s) \sum_{s^{'}}P(s^{'}|s,a)\left [ R(s,a,s^{'}) + \gamma V^{\pi}(s^{'}) \right ] $

행동 가치 함수:
$ Q^{\pi}(s,a) = \sum_{s^{'}} P(s^{'}|s,a)\left [ R(s,a,s^{'}) + \gamma \sum_{a^{'}}\pi(a^{'}|s^{'})Q^{\pi}(s^{'},a^{'}) \right ] $

$ V^{\pi}(s) $ 

상태 s의 가치로, 주어진 정책 $ \pi $를 따를 때 상태 s에서 시작하여 얻을 것으로 기대되는 총 보상의 현재 가치

$ \pi(a|s) $

정책 $ \pi $가상태 s에서 행동 a를 선택할 확률이다. 정책은 각 상태에서 어떤 행동을 취할지 결정하는 확률분포

a

에이전트가 선택할 수 있는 행동

$ \sum_{a} , \sum_{s} $

상태 a, s에서 가능한 모든 행동에 합을 구한다.

$ P(s^{'}|s,a) $

상태 s에서 행동 a를 했을 때, 다음 상태 $ s^{'} $ 로 전이될 확률이다. 이는 상태 전이 확률 로 불린다.

$ R(s,a,s^{'}) $

상태 s에서 행동 a를 취했을 때, 다음 상태 $ s^{'} $로 전이

$ \gamma $

할인 인수(discount factor)로, 미래 보상의 현재 가치에대한 가중치를 나타낸다.

감마는 0과 1 사이를 가지며 미래보상이 현재 보상에 비해 얼마나 중요한지를 나타낸다.

벨만 방정식은, 정책 파이를 따를 때 상태 또는 행동의 가치를 나타내는 방정식이다.

상태가치 함수는 특정 상태의 가치를 나타내며, 행동 가치 하뭇는 특정 상태에서 특정 행동의 가치를 나타낸다.

이러한 방정식들은 상태, 행동, 보상, 전이확률, 할인인수 등을 통해 상태 또는 행동의 기대가치를 계산하는데 사용된다.

기본골자는 다이스트라 방식과 같다. 해당 방식을 이해하고 있다면 쉽게 납득할 수 있다.

개요

문제를 해결할 때 각 단계에서 다음 단계를 검색하고, 가장 최적이라고 생각되는 선택을 하는 방식이다.

전체문제를 최적으로 해결하는데 중점을 두기 보단, 현재 각 순간마다의 선택을 최적화하는데 초점을 맞춘다.

원리

간단한 행동 원리를 가지고 있다.

상 하 좌 우 로 이동하는 알고리즘을 작성하였다고 가정한다.

상 하 좌 우 로 이동할 때 가중치를 가지고 가장 큰 가중치를 가진 방향으로 엑터는 움직이게 된다.

처음 시작시 모든 노드의 상 하 좌 우 가중치는 0이다.

같은 가중치를 가질 경우 무작위 방향으로 이동한다.

목표지점에 도달하였을 경우, 임의의 함수를 사용하여 해당 방향에 ENd가 존재함을 기입한다.

Greedy Action은 다양한 Action으로 연결되어진다. 예시를 들어 확인해보자.

위 지도를 기준으로 Start가 End로 이동하는것 이 목표라고 가정하자. Start지점에서 End로 이동해야 성공한다.

처음에는 무작위로 Start가 이동할 것이다. 1Action이 완료되었고, 이동방향이 결정되었음을 다음 으로 확인해보자.

위와같이 이동에 성공하면, End의 바로 밑 단계에는 위로 이동하면 End가 존재한다고 방향에 1을 표기한다.

1Action이 완료되었음으로 2Action을 진행한다.

2Action에서 진행하였을 때, 오른쪽 노드의 최대값이 1 임을 확인할 수 있다.

여기에서 1이 존재하는 노드가 있음으로, 저 상황에서  엑터가 오른쪽으로 이동함을 예상할 수 있다.

오른쪽으로 이동할 때, 엑터는 자기자신의 위치에 오른쪽에 1이 있다고 표시하고 이동하게 된다.

이러한 방식을 반복해서, Start와 End를 반복하였을 때 천번, 만번 반복해도 같은 결과가 나타나는 연결경로가 생겼다고 생각하자. 이것이 기본적인 Greedy Action이다.

그러나, 여기에서 무언가 찜찜함을 알 수 있는데, 최단경로는 Start에서 End로 이동하기만 하면 나타나는게 최단경로인데,

학습결과상 일단 End로 도달하기는 하나 최적의 경로는 아니라는 점이다.

이를 해결하기 위해 다음 방식들을 추가한다.

탐험 Exploration

입실론 - Greedy

입실론 ; 0 ~ 1 만큼은 랜덤!

랜덤한 확률로 가중치에 해당되는 이동경로로 가지 않고 무작위로 선택된 이동경로로 이동하게 하는것 을 의미한다.

탐험하면서 새로운 가중치를 확인하고. 더 나은 경로를 찾을 수 있기 때문이다.

Exploration & Exploitation

Exploration

장점

새로운 경로를 찾을 수 있다.

새로운 End를 찾을 수 있다.

(Decaying) 입실론 - Greedy

처음에는 입실론 값을 0.9 정도로 잡다가. 어느정도 값이 잡히게 되면 0으로 수렴하게 한다.

그러나, 여기에서는 더 가까운 경로를 찾을 수 없을지도 모른다는 가능성이 생긴다.

Discount Factor

수학적인 수렴성에 있다.

감마 라는걸 추가하게 되는데 이는 다음과 같다.

감마 : 효율적인 패스를 찾게 해준다. 0 ~1 사이의 값이다.

바로 다음노드의 값을 가져오게 될때 는 감마를 곱해서 가져와라 라는 의미이다.

만약, 소숫점이 0.5라고 가정하면 1에서 0.5를 곱해서 가져오고.. 가져오고...가져오고 를 반복하게 됨으로

거리가 멀어질 수록 값이 점점 0에 가까워질것이다.

그럼으로써 거리값에 따라 멀수록 0에 수렴. 가까울수록 1에 수렴하게 된다.

엑터는 이로써 거리값에 따른 가중치를 판별할 수 있다.

장점

효율적인 Path를 가져올 수 있다.

현재 vs 미래 reward를 할 수 있다.

즉, 감마가 작을 수록 미래에 대한 가중치를 덜 확인한다. 설레발을 덜친다.

수식

$Q\left ( S_{t},Q_{t} \right )\leftarrow \left ( 1-\alpha \right )Q\left( S_t,Q_t\right ) + \alpha (R_t + \gamma  maxQ(S_t{''},Q_t{''}))$

쓰잘데기없이 복잡하게 되어있는데, 쉽게 말하면

현재 노드 = (1-가중치) * 현재값 + (가중치) * (시간상수[감마] * 미래값)

을 말한다.