https://learn.microsoft.com/ko-kr/cpp/mfc/device-contexts?view=msvc-170&redirectedfrom=MSDN 

Windows 데이터 구조로서, 디바이스의 그리기 특성에 대한 정보를 포함한다.

디바이스 컨텍스트를 활용하여 화면, 프린터 또는 메타파일로 그릴 수 있다.

위 항목에서 참조하면 자세한 설명을 확인할 수 있지만, 축약하자면.

CPaintDC 개체가 Windows의 어려운부분을 캡슐화하여 가지고있고, 그 함수를 호출하고, 객체를 관리하는 역활을 한다.

CClientDC 개체는. 창의 클라이언트 영역을 나타내는 디바이스이고, 이것은 캡슐화되어 있다. 창을 관리한다.

CMetaFildeDC는, 드로잉 된 파일을 WIndows의 메타파일로 캡슐화 하여 가공하는 역활을 한다.

Queue_by_LinkedList

큐는 선형 데이터 저장방식 중 하나로, FIFO구조를 따르며, 선입선출 방식으로 데이터를 기입하고 호출하게 된다.

이러한 큐 구조를 리스트 방식으로 제작할 수 있다.

이러한 큐의 저장방식은 연결리스트 를 통하여 구현하고, Queue라는 Class를 만들어서, 전체 큐의 사이즈, 연결된 부위, 삭제, 기입, 추출 등의 작업을 수행한다.

#include <iostream>

using namespace std;

template<typename T>
class Queue
{
public:
	struct Node
	{
		T Data;
		// 단일연결 리스트 를 통해 구현
		Node* Next;
		//큐 에서는 넣고 빼고 지우고 가능하다. 구현한다.
	};

private:
	int count = 0;
	// 보관 개수

	Node* front = NULL;// 가장 앞 변수 만들고 NULL로 초기화
	//Q 는 FIFO 구조 이기 때문에 front는 빼낼 값.
	Node* rear = NULL;

public:
	Queue() {}

	~Queue()
	{

	}

	void Enqueue(Node* node)
	{
		if (front == NULL)
		{
			// 비어있는 경우 에는,
			front = node;
			rear = node;
			// 처음과 끝을 한개의노드로 정해준다.
			count++; // count 에 1을 해서 1개라고 표시

			return;
		}

		rear->Next = node; // 한개 추가하면, 뒤의 다음값은, node가 되어야 한다.
		rear = node;// 뒤를 node로 설정해준다.

		count++;
	}

	Node* Dequeue()
	{
		// 노드를 제거하고 반환하는 형식을 만든다.
		Node* node = front;// 큐에서 제거해서 반환될 노드
		if (front->Next == NULL) // 큐에 남은 값이 없을 경우.
		{
			front = rear = NULL;
		}
		else
		{
			front = front->Next; // 큐가 한개초과 일 경우, Next를 front로 넣어준다.
		}

		count--;

		return node;
	}

	int Size() { return count; }

	bool IsEmpty() {
		return front == NULL; // 비어있는지 확인
	}
public:
	static Node* CreateNode(T data)
	{
		Node* node = new Node();
		node->Data = data;
		node->Next = NULL;

		return node;
	}

	static void DestroyNode(Node** node)
	{
		delete* node;
		*node = NULL;
	}
};

int main()
{
	Queue<int> queue;
	queue.Enqueue(Queue<int>::CreateNode(10));
	queue.Enqueue(Queue<int>::CreateNode(20));
	queue.Enqueue(Queue<int>::CreateNode(30));

	cout << "Size : " << queue.Size() << endl;

	while (queue.IsEmpty() == false)
	{
		Queue<int>::Node* node = queue.Dequeue();
		cout << "Dequeue : " << node->Data << endl;

		Queue<int>::DestroyNode(&node);
	}
	return 0;
}

위 방식으로 Queue를 직접 구현해줄 수 있다.

Tree

트리구조는, 기본적인 비선형 데이터 저장방식으로써, 계층적인 데이터를 표현하기 위해 사용된다.

노드들이 부모 - 자식 관계로 연결되어 있으며, 최상위 노드로부터 파생되어 내려온다.

트리구조의 장점

• 데이터의 구조와 관계를 직관적으로 이해할 수 있다.
• 데이터의 삽입, 삭제 검색이 매우 빠르게 이루어진다.
• 정렬, 탐색, 필터링 등의 작업에 유용하다.

트리구조의 단점

• 데이터의 삽입, 삭제 시에 트리구조의 재정렬이 필요하기 때문에 추가작업이 필요할 수 있다.
• 트리구조를 메모리에 저장하기 위해 포인터 구조를 사용할 경우, 추가적인 메모리공간을 사용한다.
• 트리구조가 변경될 경우, 전체 트리구조를 변경해야하는 번거로움이 있다.

#include <iostream>
#include <stack>
#include <queue>
// 기본적인 트리구조 구축
using namespace std;

template<typename T>
class Tree
{
public:
	struct Node
	{
		T Data;

		Node* LeftChild;
		Node* RightSibling;
		~Node()
		{
			Data = 0;

			LeftChild = NULL;
			RightSibling = NULL;
		}
	};
public:
	stack<Node*>* Stack() { return &stack; }
	queue<T>* Queue() { return &queue; }
private:
	queue<T> queue;
	// 출력하는데 활용
	stack<Node*> stack;
	// 트리노드 순회, 노드 삭제하는데 활용
public:
	static Node* CreateNode(T data)
	{
		Node* node = new Node();
		node->Data = data;
		node->LeftChild = node->RightSibling = NULL;

		return node;
	}

	static void DestoryNode(Node** node)
	{
		delete* node;
		*node = NULL;
	}
public:
	void Addchild(Node* parent, Node* child)
	{
		if (parent->LeftChild == NULL)
		{
			parent->LeftChild = child;
			
			return;
		}

		Node* node = parent->LeftChild;
		
		while (node->RightSibling != NULL)
		{
			node = node->RightSibling;
			// 노드의 오른쪽으로 계속 이동
		}

		node->RightSibling = child;
		// 계속 이동한 노드의 최우측끝 에 값을 삽입한다.
	}

	void PrintNode(Node* node, int depth)
	{
		for (int i = 0; i < depth; i++)
			cout << "-";

		cout << node->Data << endl;
		queue.push(node->Data);
		stack.push(node);

		if (node->LeftChild != NULL) // leftChild가 있는지 확인 있다면, 제귀
			PrintNode(node->LeftChild, depth + 1);

		if (node->RightSibling != NULL) // 오른쪽이 존재하는지 확인, 있다면 제귀
			PrintNode(node->RightSibling, depth);
	}
};

int main()
{
	Tree<char> tree;

	Tree<char>::Node* A = Tree<char>::CreateNode('A');
	Tree<char>::Node* B = Tree<char>::CreateNode('B');
	Tree<char>::Node* C = Tree<char>::CreateNode('C');
	Tree<char>::Node* D = Tree<char>::CreateNode('D');
	Tree<char>::Node* E = Tree<char>::CreateNode('E');
	Tree<char>::Node* F = Tree<char>::CreateNode('F');
	Tree<char>::Node* G = Tree<char>::CreateNode('G');
	Tree<char>::Node* H = Tree<char>::CreateNode('H');
	Tree<char>::Node* I = Tree<char>::CreateNode('I');
	Tree<char>::Node* J = Tree<char>::CreateNode('J');
	Tree<char>::Node* K = Tree<char>::CreateNode('K');

	tree.Addchild(A, B);
	tree.Addchild(B, C);
	tree.Addchild(B, D);
	tree.Addchild(D, E);
	tree.Addchild(D, F);

	tree.Addchild(A, G);
	tree.Addchild(G, H);

	tree.Addchild(A, I);
	tree.Addchild(I, J);
	tree.Addchild(I, K);

	tree.PrintNode(A, 0);

	while (tree.Queue()->empty() == false)
	{
		cout << tree.Queue()->front() << endl;
		tree.Queue()->pop();
	}
	cout << endl << endl;

	while (tree.Stack()->empty() == false)
	{
		Tree<char>::Node* node = tree.Stack()->top();
		tree.Stack()->pop();

		Tree<char>::DestoryNode(&node);
	}

	return 0;
}

위 방식대로 트리구조를 직접 제작하여 사용할 수 있다.

Stack

스텍은 데이터를 후입선출(FIFO) 방식으로 관리하는 자료구조 로, 데이터를 저장하고 검색작업을 수행하는데 사용된다.

스텍의 특징

• 삽입과 삭제가 제한적이다.
  • 한쪽끝에서만 삽입 삭제가 가능한데, 이것은FIFO구조로 관리하기 때문이다. 스택은 맨위에 추가되며, 가장 위의 요소만을 제거할 수 있다.
• 접근이 제한적이다.
  • 스택은 가장 위에있는 요소에만 접근, 추가, 삭제 할 수 있다.

스텍의 장점

• 구조가 직관적이고 단순하다.
• 메모리를 효율적으로 활용할 수 있다.
• 재귀 알고리즘을 구현하는데 사용할 수 있다.
  • 재귀호출 상태를 스택에 저장하여, 알고리즘의 진행과 복귀를 관리할 수 있다.

스텍의 단점

• 고정된 크기를 가지고 있어, 데이터의 개수가 스텍의 크기를 초과하면, 오버플로우가 발생한다.
• 중간요소에 접근하기가 힘들다.

Stack의 알고리즘 구현,

#include <iostream>
#include <memory.h>
#include <cassert>

using namespace std;

#define MAXSTACKCOUNT 20

template<typename T>
class Stack
{
private:
	int top = -1;
	T values[MAXSTACKCOUNT];
public:
	Stack()
	{
		memset(values, 0, sizeof(T) * MAXSTACKCOUNT);
		// 메모리 초기화 해주는 함수.
		// 메모리 시작 주소 기입,
		// 메모리 사이즈 기입한다.
		// 0으로 모든 메모리를 초기화해주는 함수,
	}

	void Push(T value)
	{
		assert(top + 1 < MAXSTACKCOUNT);
		// Stack이 가득차지 않았다면,
		values[++top] = value; // values라는 배열에 1씩 더해주면서 올려준다.
	}
	T Pop()
	{
		assert(Empty() == false);

		T val = values[top--];

		return val; // 맨 위의 요소를 제거하고 그 요소를 반환해준다.
	}
	T Front()
	{
		return values[top]; // 맨 위의 값을 반환해준다.
	}
	T back()
	{
		assert(top > -1);
		return values[0]; // 배열의 가장 뒤의 값을 반환한다.
		// 배열이 비어있는지 또한 확인한다.
	}

	bool Empty()
	{ // 배열이 비어있는지, top이 0보다 작으면 비어있다는 의미 이기 때문에,
		return top < 0 ? true : false;
	}
};

int main()
{
	Stack<int> stack;

	stack.Push(10);
	stack.Push(20);
	stack.Push(30);
	stack.Pop();

	stack.Push(40);
	stack.Push(50);

	cout << stack.back() << endl << endl;
	cout << stack.Front() << endl << endl;

	while (stack.Empty() == false)
		cout << stack.Pop() << endl;

	return 0;
}

Linkedlist_Stack

일반적으로, 스텍은 데이터의 저장공간이 한정적이다.

그러나, 리스트배열 방식으로 스텍을 관리하여, 저장공간을 유동적으로 바꾸어 줄 수 있다.

#include <iostream>

using namespace std;

struct Node
{
	int Data;

	Node* NextNode;
};

class Stack
{
private:
	Node* list = NULL; // 스텍의 배열을 가리킴
	Node* top = NULL; // 스텍의 제일위 요소 가리키게 만듬

public:
	Stack();
	~Stack();

	void Push(Node* node);
	Node* Pop();

	int Size();
	bool IsEmpty();

	static Node* CreateNode(int data);
	static void DestoryNode(Node** node);
};

Stack::Stack()
{}
Stack::~Stack()
{
	// pop을 계속 호출함으로써 모든 스텍을 제거하도록 만든다.
	while (IsEmpty() == false)
	{
		Node* node = Pop();
		DestoryNode(&node);
	}
	list = NULL;
	top = NULL;
}

void Stack::Push(Node * node)
{
	if (list != NULL) // 현재 스텍이 비어있지 않다면,
	{
		Node* tail = list; // 스텍의 끝 까지 이동할 포인터.
		// 마지막에서 끝부분에 값을 넣는다.
		while (tail->NextNode != NULL)
			tail = tail->NextNode;

		tail->NextNode = node;
		// tail 의 마지막 NULL에 node를 연결한다.
	}
	else // 스텍이 비어있다면
	{
		list = node;
	}
}

Node* Stack::Pop()
{
	// 데이터를 반환하고 날리면 된다.
	if (list == top) // 배열이 한개뿐 이라면,
	{
		list = NULL;
		top = NULL;
	}
	else
	{
		Node* tail = list;
		while (tail != NULL && tail->NextNode != top)
		{
			tail = tail->NextNode;
		}

		top = tail;
		// 맨위 노드와의 연결을 분리하고,
		// 맨 위 노드를 반환한다.
		tail->NextNode = NULL;
	}

	return top;
}

int Stack::Size()
{
	int count = 0;
	Node* node = list;

	while (node != NULL)
	{
		node = node->NextNode;
		count++;
	}
	return count;
}

bool Stack::IsEmpty()
{
	return list == NULL;
}

Node* Stack::CreateNode(int data)
{
	Node* node = new Node();
	node->Data = data;
	node->NextNode = NULL;
	// 만들어졌을 때는 다음 노드가 없음으로 NULL로 처리
	return node;
}

void Stack::DestoryNode(Node** node)
{
	delete* node;
	*node = NULL;
	// 데이터를 해제하기 위해서 이중포인터로 가져와야 한다.
}


int main()
{
	Stack stack;
	stack.Push(Stack::CreateNode(10));
	stack.Push(Stack::CreateNode(20));
	stack.Push(Stack::CreateNode(30));
	stack.Push(Stack::CreateNode(40));

	int count = stack.Size();
	cout << "Size : " << count << endl;

	for (int i = 0; i < count; i++)
	{
		if (stack.IsEmpty() == true)
			break;

		Node* temp = stack.Pop();
		cout << "pop : " << temp->Data << endl;
		Stack::DestoryNode(&temp);
	}


	return 0;
}

Breadth_First_Search

너비우선 탐색은, 그래프 탐색 알고리즘 중 하나로, 그래프의 노드들을 너비 우선으로 탐색하는 방법이다.

BFS는, 그래프의 구조를 확인한 뒤, 임의의 두 노드 간의 최단경로를 찾는 등의 문제를 해결하는데 사용된다.

BFS의 장점

• 그래프 상의 최단거리를 찾는데 효과적이다.
• 재귀적으로 동작하지 않고, 큐를 통해 구현됨으로 메모리관리 측면에서 효율적이다.
• 그래프에 순환경로가 없다면, 모든 노드 방문이 가능할 수 있다.

BFS의 단점

• 모든 인접 노드를 방문해야 하기 때문에, 그래프가 매우 큰 경우 탐색시간과 메모리 사용량이 증가할 수 있다.
• BFS는 깊이 우선 탐색(DFS)에 비해, 경로를 찾는데에 더 많은 메모리를 요구한다. 큐에 모든 인접노드 정보를 저장해야하기 때문,

정리

Breath_First_Search는, 너비우선으로 진행하여 모든 노드를 탐색하는 알고리즘이다.

시작노드 로 부터 인접한 노드를 차례로 방문하여, 최단경로를 찾는데 사용된다.

시작노드로부터 인접한 노드를 탐색하면서, 깊게 들어가는것 이 아닌, 같은 깊이의 노드들을 모두 방문한 다음, 다음 깊이의 노드로 넘어간다.

그럼으로, 시작노드와 가까운 노드부터 방문하게 되어 최단경로를 빠르게 찾을 수 있게된다.

코드 예시

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// 먼저 방문한 노드의 상하좌우를 먼저 탐색하고.
// 전부 탐색한 다음 노드로 처리하러 이동한다.
// FIFO구조.

bool visited[9];
vector<int> graph[9];

void bfs(int start) // 시작 노드를 넣어주고 시작한다.
{
	queue<int> q;
	q.push(start); // 시작노드 넣어줌.
	// 이 시작노드는 방문처리가 된다.
	visited[start] = true;
	// 방문했다는 의미를 가지는 배열을 따로 만들어준다.

	while (!q.empty()) {
		int x = q.front();
		// 가장 앞의 요소. 가장 오래된 요소. 가져옴
		// 가장 처음 들어간 요소

		q.pop(); 
		// 가져온다음 빼준다.
		cout << x << ' ';

		for (int i = 0; i < graph[x].size(); i++)
		{// 현재 순환하는 graph의 size를 탐색한다.
		 // 그 후, 해당 graph에 연결되어있는 노드를전부 탐색
			int y = graph[x][i];
			// y 에 해당 번째의 i를 박아넣는다.
			if (!visited[y])
			{// 만약, 해당번째의 i가 방문한적 이 없다면,
				q.push(y);
				// q에 push하여 넣어주고,
				visited[y] = true;
				// 방문록을 작성한다.
			}
		}
	}
}

int main()
{
	graph[1].push_back(2);
	graph[1].push_back(3);
	graph[1].push_back(8);

	graph[2].push_back(1);
	graph[2].push_back(7);

	graph[3].push_back(1);
	graph[3].push_back(4);
	graph[3].push_back(5);

	graph[4].push_back(3);
	graph[4].push_back(5);

	graph[5].push_back(3);
	graph[5].push_back(4);

	graph[6].push_back(7);

	graph[7].push_back(2);
	graph[7].push_back(6);
	graph[7].push_back(8);

	graph[8].push_back(1);
	graph[8].push_back(7);

	bfs(1);

	return 0;
}

위 코드에서 1부터 가장 좌측 노드부터 탐색함으로,

1, 2, 3, 8 이 출력되고 2의 가장 가까운 7,

그이후 3의 4, 5

8은 이미 7을 탐색했음 으로 생략,

그리고 7의 6 이 출력됨으로

결과는 1238756이 나타나게 된다.

BruteForce

무차별 대입법(BruteForce) 은 완전탐색 알고리즘 으로, 가능한 모든 경우의 수를 전부 탐색하여

정확한 해답을 찾는 방법이다. 이 방법은 모든 가능한 조합을 검사하기 때문에, 시간이 오래걸림으로

큰 입력값, 매우 넓은 범위를 탐색하는것 에 대해서는 매우 비효율적이다.

그러나, 직관적인 방식으로 탐색하기 때문에 쉽게 문제를 해결할 수 있다.

다음은 BruteForce를 구현한 알고리즘으로, 10개의 숫자중 8개의 숫자를 더했을 때 100이 나오는 경우를 구하는 코드 이다.

#include <iostream>
#include <list>

using namespace std;

// 무식하게 탐색한다.
// 완전탐색 알고리즘.
// 모든 경우의 수를 전부 탐색한다.
// 백트래킹 = 의미없는 경우는 제외하고 전부 탐색한다.
// 진행하는게 의미없는 조건을 찾아야 한다.

// 제외해줘야 하기 때문에 처리 자체가 불가능 해질 수 있다.

/*
	10개의 숫자가 있다.
	7 15 21 8 14 25 10 11 17 5

	이 중 숫자가 딱 100이 되는 8개의 숫자 찾기
	예외처리 해주면서,
	어떻게 해줘야 최대한 이 반복문을 줄일 수 있는지 생각해보기.

	의미 없는 경우
	
	배열은 먼저 sort한 뒤, 작은숫자대로 더한다.
	그러나 남은 덧셈 수가 남아있는수 보다 작을 경우 의미가 없기 때문에 전 수는 빼낸다.
	빼낸 뒤 나머지를 덧셈 해준다.

	왼쪽부터 오른쪽까지 다 계산해야한다.

	왼쪽부터 다 더하면서 가다가 결과가 안나왔을 시 전 것을 빼고 바로 다음꺼를 더해서 계산

	순방향 정렬을 한 뒤 완전탐색을 시도하였을 경우,
	임의의 모든 값을 순환시키는것 보다 약 O^n/2 만큼 더 줄어들 수 있다.

*/

auto Chack_dup(int arr[] ,int size ,int a) -> bool
{
	for (int i = 0; i < size; i++)
		if (arr[i] == a) return false;
	return true;
}

auto Array_Sum(int arr[], int size) -> int
{
	int result = 0;
	for (int i = 0; i < size; i++) result += arr[i];
	return result;
}

auto PRINT(int arr[], int size, string str) -> void
{
	cout << str;

	for (int i = 0; i < size; i++) {
		if (arr[i] != 0) cout << arr[i] << " ";
	}

	cout << "\tSUM : " << Array_Sum(arr, size) << endl;
}

auto BruteForce(int arr[], int start, int end, int count = 0) -> bool
{
	static int result[8] = { 0 };
	static int stic_i = 0;
	// 10^10 차원의 8개의 점으로 이루어진 선 한줄을 찾아야한다.
	for (int i = start; i <= end; i++) { // 10^10차원을 제귀를 통해 전개한다.
		if (count == 8) break; // count == 8 이 됨은, 들어간 배열이 가득 찼다는 의미이다. 그럼으로 전개된 차원을 탈출
		if (Chack_dup(result, 8, arr[i])) { // 중복값을 체크하여, 현재값에 진입해 있는지 확인한다.
			result[count] = arr[i]; // 현재 차원위치에 지정된 값을 삽입해준다.
			BruteForce(arr, start + 1, end, count + 1); // 재귀를 사용하여 다음 차원위치로 이동해준다.
		}
	}

	int Asum = Array_Sum(result, 8); // 현재 결과에 있는 모든 데이터를 더해준다.

	if (Asum == 100) { // 모든 데이터를 더했을 때 100이 나올경우,
		PRINT(result, 8, "RESULT : "); exit(0); // 결과를 출력해주고 1을 반환한다.
	}

	if (start >= end) { return 0; } 
	// start가 end보다 크거나 같을경우, 10^10 차원순환이 전부 완료되었을 경우, 
	// 순환완료한 재귀의 기입된 배열데이터는 의미가 없어지기 때문에 0을 반환하고 종료해준다.
	else if (Asum != 100 && count == 8) {
		// Asum 이 100이 아니고 count가 8일경우, 위의 if문에 해당이 안되기 때문에 차원순환이 전부 종료되지 않아
		// 남은 차원을 전부 순환시켜주어야 한다.
		result[count] = 0; // 현재 가득 찬 배열은 100을 만들어내지 못함으로 0으로 초기화시켜준다.
		BruteForce(arr, start + 1, end, count - 1);
		// 현재 남은 배열을 전부 순환시켜주기 위해 count를 1 줄여 마지막 값을 다음으로 넘길 수 있게 하고,
		// 다음 배열위치로 넘겨준다.
	}

	return 0;
}

int main()
{
	int arr[] = { 7, 15, 21, 8, 14, 25, 10, 11, 17, 5 };
    BruteForce(arr,0, 9);
	return 0;
}

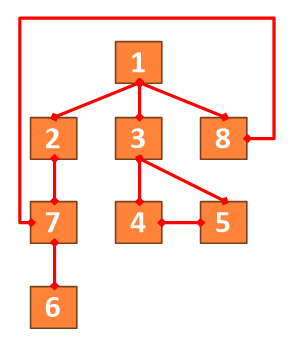
Depth_first_search

그래프를 탐색하는 알고리즘 중 하나로, 시작 노드 에서 탐색을 시작하여, 다음 노드로 계속해서 탐색을 진행하며,

더이상 탐색할 수 없는 상태까지 깊이 들어가면 이전 단계로 돌아와, 다른 경로를 탐색한다.

이것을 반복하여 그래프를 탐색하는 방식이다.

DFS 알고리즘의 특징은 다음과 같다.

• 깊이 우선 탐색은 스택 또는 재귀 함수를 사용하여 구현할 수 있다.
• 탐색 도중에 더이상 가갈 수 없는 경로가 없다면, 이전단계로 돌아가 다른 경로를 탐색한다.
• DFS는 깊이에 우선순위를 두기 때문에 시작 노드와 가까운 노드를 먼저 탐색하게 된다.

DFS 알고리즘의 장점은 다음과 같다.

• 구현이 간단하고, 직관적이다.
• 노드를 방문하는 순서를 추적할 수 있음으로 경로를 복구하는데 유효하다.
• 그래프에서 연결된 모든 구성요소를 탐색할 수 있다.

DFS 알고리즘의 단점은 다음과 같다.

• 그래프에 순환 경로가 있는 경우, 무한루프에 빠질 수 있다.
• 그래프가 매우 깊거나 무한한 경우, 탐색경로가 길어지기 때문에 스택 오버플로우(Stack Overflow)가 발생할 수 있다.
• 최단 경로를 찾는것과 같이. 최적의 해를 찾는 문제에는 적합하지 않다.

DFS 알고리즘은 다음 상황에서 사용된다.

• 그래프에서 한노드부터 연결된 모든 노드를 탐색해야 할 경우.
• 어떠한 반복되는 노드 간의 사이클을 탐지해야 할 경우,
• 시작 노드에서 목표 노드까지의 경로를 찾아야 할 경우,
• 트리구조 일 경우, 모든 트리를 탐색할 경우.

DFS 알고리즘 의 코드 예시는 다음과 같다.

#include <iostream>

using namespace std;

// 깊이 우선 탐색
// 내가 갈 수 있는 대로 최대한 들어가는 방식.
// 불필요한 경우를 차단하거나 그런건 없다.
// 그래서 경우의 수를 줄일 수 없다.
// 제귀로 들어가는 방법과 스텍으로 들어가는 방법이 있다.

template<typename T>
class Graph
{
public:

	struct Node;
	struct Edge // 간선 제작
	{
		Node* Start = NULL;
		Node* Target = NULL;
		Edge* Next = NULL;
	};
	struct Node
	{
		T Data;
		int Index = -1;
	
		Node* Next = NULL; // 다음 노드에 대한 포인터
		Edge* Edge = NULL; // 다음 간선에 대한 포인터
		
		bool Visited = false; // 방문 여부에 대한 결과
	};

private:
	Node* Head = NULL;
	int Count = 0;

public:
	static Edge* CreateEdge(Node* start, Node* target)
	{
		Edge* edge = new Edge(); // 동적할당.
		edge->Start = start;
		edge->Target = target;

		return edge;
	}
	static Node* CreateNode(T data)
	{
		Node* node = new Node();
		node->Data = data;

		return node;
	}

public:
	void AddNode(Node* node)
	{
		Node* nodeList = Head; // Head = 연결리스트에서 머리를 구현한다.

		if (nodeList != NULL)
		{
			while (nodeList->Next != NULL)
			{
				nodeList = nodeList->Next;
			}
			nodeList->Next = node; // 새로운 노드가 연결리스트 끝에 위치하게 된다.
		}
		else
		{
			Head = node;
		}

		node->Index = Count++;
	}

	void AddEdge(Node* node, Edge* edge)
	{
		if (node->Edge != NULL)
		{
			Edge* edgeList = node -> Edge;
			while (edgeList->Next != NULL)
			{
				edgeList = edgeList->Next;
			}

			edgeList->Next = edge;
		}
		else
		{
			node->Edge = edge;
		}
	}

	void Print()
	{
		Node* node = NULL;
		Edge* edge = NULL;
		if((node = Head) == NULL) // 헤드가 없다면 정보가 없으니까 종료
			return;
		while (node != NULL)
		{
			cout << node -> Data << " : ";
			if ((edge = node->Edge) == NULL)
			{
				node = node->Next;
				cout << endl;

				continue;
			}

			while (edge != NULL)
			{
				cout << edge->Target->Data;
				edge = edge->Next;
			}

			cout << endl;

			node = node->Next;
		}

		cout << endl;
	}

	void DFS(Node* node)
	{
		cout << node->Data;

		node->Visited = true;

		Edge* edge = node->Edge;

		while (edge != NULL)
		{
			if(edge->Target != NULL && edge->Target->Visited == false)
				DFS(edge->Target);
			edge = edge->Next; // 간선이 하나가 아니기 떄문에, 다음 간선도 체크해주는 부분을 만들어주어야 한다.
		}
	}
};

typedef Graph<char> G;

int main()
{
	G graph;

	G::Node* n1 = G::CreateNode('A');
	G::Node* n2 = G::CreateNode('B');
	G::Node* n3 = G::CreateNode('C');
	G::Node* n4 = G::CreateNode('D');
	G::Node* n5 = G::CreateNode('E');

	graph.AddNode(n1);
	graph.AddNode(n2);
	graph.AddNode(n3);
	graph.AddNode(n4);
	graph.AddNode(n5);
	
	graph.AddEdge(n1, G::CreateEdge(n1, n2));
	graph.AddEdge(n1, G::CreateEdge(n1, n3));
	graph.AddEdge(n1, G::CreateEdge(n1, n4));
	graph.AddEdge(n1, G::CreateEdge(n1, n5));
	
	graph.AddEdge(n2, G::CreateEdge(n2, n1));
	graph.AddEdge(n2, G::CreateEdge(n2, n3));
	graph.AddEdge(n2, G::CreateEdge(n2, n5));

	graph.AddEdge(n3, G::CreateEdge(n3, n1));
	graph.AddEdge(n3, G::CreateEdge(n2, n2));

	graph.AddEdge(n4, G::CreateEdge(n4, n1));
	graph.AddEdge(n4, G::CreateEdge(n4, n5));

	graph.AddEdge(n5, G::CreateEdge(n2, n1));
	graph.AddEdge(n5, G::CreateEdge(n2, n2));
	graph.AddEdge(n5, G::CreateEdge(n2, n4));

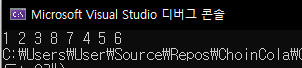
	graph.Print();

	graph.DFS(n1);







	return 0;
}

위 코드는 graph 라는 하나의 구조체를 생성한 뒤, 구조체 안에 모든 함수를 구현한 형태이다.

충돌체 처리를 위해, Physics 를 활용하여 QuadColider, CircleColider 을 제작한다.

#pragma once

#include "Engine/Input.h"
#include "Engine/Physics.h"
#include "Engine/Quadrangle.h"
#include "Engine/Rendering.h"
#include "Engine/Time.h"

struct QuadColider
{
	QuadColider()
	{
		Skin.Length = { 250, 250 };
		Skin.Location = { 300, 0 };
		Skin.Name = "Image/GBB";

		Body.Length = { 250, 250 }; // 충돌체의 모양
		Body.Center = { 300, 0 }; // 충돌체 방향 잡는것.
	}

	void Update()
	{
		if(Engine::Input::Get::Key::Press(VK_NUMPAD4))
			Skin.Location[0] = Body.Center.x -= Speed * Engine::Time::Get::Delta();
		if (Engine::Input::Get::Key::Press(VK_NUMPAD6))
			Skin.Location[0] = Body.Center.x += Speed * Engine::Time::Get::Delta();
		if (Engine::Input::Get::Key::Press(VK_NUMPAD8))
			Skin.Location[1] = Body.Center.y += Speed * Engine::Time::Get::Delta();
		if (Engine::Input::Get::Key::Press(VK_NUMPAD2))
			Skin.Location[1] = Body.Center.y -= Speed * Engine::Time::Get::Delta();

		Skin.Render();
	}

	float const Speed = 500;
	Engine::Rendering::Image::Component		Skin{};
	Engine::Physics::Component<Quadrangle>	Body{};

};

#pragma once

#include "Engine/Input.h"
#include "Engine/Physics.h"
#include "Engine/Circle.h"
#include "Engine/Rendering.h"
#include "Engine/Time.h"

struct CircleColider
{
	CircleColider()
	{
		Skin.Length = { 250, 250 };
		Skin.Location = { -300, 0 };
		Skin.Name = "Image/GBC";

		Body.Radius = 125;
		Body.Center = { -300, 0 }; // 충돌체 방향 잡는것.
	}

	void Update()
	{
		if (Engine::Input::Get::Key::Press('A'))
			Skin.Location[0] = Body.Center.x -= Speed * Engine::Time::Get::Delta();
		if (Engine::Input::Get::Key::Press('D'))
			Skin.Location[0] = Body.Center.x += Speed * Engine::Time::Get::Delta();
		if (Engine::Input::Get::Key::Press('W'))
			Skin.Location[1] = Body.Center.y += Speed * Engine::Time::Get::Delta();
		if (Engine::Input::Get::Key::Press('S'))
			Skin.Location[1] = Body.Center.y -= Speed * Engine::Time::Get::Delta();

		Skin.Render();
	}

	float const Speed = 500;
	Engine::Rendering::Image::Component	Skin{};
	Engine::Physics::Component<Circle>	Body{};

};

위 항목의 CircleColider 와 QuadColider의 코드는 비슷함 으로 CircleColider 기준으로 설명한다.

CircleColider는 struct로 구성되어 있으나, 생성시 자동으로 선언되는 함수인 생성자 를 만들어줄 수 있다.

생성자는 public에 해당하는, 외부이미지의 Skin과 PhysicsColider를 담당할 Body를 복사대입 해준다.

Skin은 이미지의 사이즈를 의미하고, Center는 이미지의 중심축을 말한다.

Body.Radius는 원형의 반지름을 말한다.

그 후, TempGame.cpp의 전역부분에 QC와 CC를 선언해준뒤,

QuadColider QC;
CircleColider CC;

중략....


	QC.Update();
	CC.Update();

	if (QC.Body.Collide(CC.Body) == true)
	{
		QC.Skin.Name = "Image/RBB";
		CC.Skin.Name = "Image/RBC";
	}
	else
	{
		QC.Skin.Name = "Image/GBB";
		CC.Skin.Name = "Image/GBC";
	}

Update부분 안에 위와같은 항목을 삽입한다.

Collide는 D3dx.dll의 항목을 의미한다.

위와같이, 각 이미지파일이 겹쳤을 때 빨간색으로 바뀌면 성공이다.

Sort 자료구조를 재구현 해보자.

/*
	Big O 표기법
	O(1), O(logn), O(n), O(nlogn), O(n^2), O(2^n), O(n!)
	
	피봇을 가장 좌측, 가장 중앙 둘중 하나로 정한다.

	L과 R이라고 하여, 왼쪽 가장 오른쪽값을 결정한다.
	
	피봇이 L과 R을 비교하여 가장작은지 큰지 확인하고
	
	더 작은쪽으로 이동한다.
	그러다가 더 큰쪽을 작은쪽과 이동한다.

*/

#include <iostream>

using namespace std;

void QuickSort(int* arr, int start, int end)
{
	if(start >= end) return;

	int pivot = start;
	int left = start + 1;
	int right = end;

	while (left <= right)
	{
		while(arr[left] < arr[pivot] && left <= end)
			left++; // 작으면 이동시킨다.
		while (arr[right] > arr[pivot] && right >= start)
			right--; // 작으면 이동시킨다.

		if(left >= right) break;

		swap(arr[left], arr[right]);
	}
	swap(arr[pivot], arr[right]);
	
	QuickSort(arr, start, right - 1);
	QuickSort(arr, right + 1, end);

}

void Print(int* arr, int size, string str)
{
	cout << str << endl;
	for(int i = 0; i < size; i++)
		cout << arr[i] << " ";
	cout << endl;

}

int main()
{
	int arr[10];
	
	for (int i = 0; i < 10; i++)
	{
		cin >> arr[i];
	}

	Print(arr, 10, "PREV : ");
	QuickSort(arr, 0, 9);
	Print(arr, 10, "NEXT : ");
	return 0;
}

위와같이, QuicKSort 코드를 사용하여 pivot값을 재설정하여 sort할 수 있다.

QuickSort

• 하나의 리스트를 피벗(pibot)을 기준으로 두개의 비균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법.
• 다음 단계들로 이루어진다.
  1. 분할(Divide) : 입력 배열을 피벗을 기준으로 2개로 (피벗 기준으로 작은건 왼쪽, 큰건 오른쪽) 분할한다.
  2. 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환호출하여 다시 분할정복 한다.
  3. 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 결합한다.
• 순환호출이 한번 진행될 때 마다, 값 하나의 위치가 정해지게 됨 으로 반드시 종료된다.