728x90
Breadth_First_Search
너비우선 탐색은, 그래프 탐색 알고리즘 중 하나로, 그래프의 노드들을 너비 우선으로 탐색하는 방법이다.
BFS는, 그래프의 구조를 확인한 뒤, 임의의 두 노드 간의 최단경로를 찾는 등의 문제를 해결하는데 사용된다.
BFS의 장점
- 그래프 상의 최단거리를 찾는데 효과적이다.
- 재귀적으로 동작하지 않고, 큐를 통해 구현됨으로 메모리관리 측면에서 효율적이다.
- 그래프에 순환경로가 없다면, 모든 노드 방문이 가능할 수 있다.
BFS의 단점
- 모든 인접 노드를 방문해야 하기 때문에, 그래프가 매우 큰 경우 탐색시간과 메모리 사용량이 증가할 수 있다.
- BFS는 깊이 우선 탐색(DFS)에 비해, 경로를 찾는데에 더 많은 메모리를 요구한다. 큐에 모든 인접노드 정보를 저장해야하기 때문,
정리
Breath_First_Search는, 너비우선으로 진행하여 모든 노드를 탐색하는 알고리즘이다.
시작노드 로 부터 인접한 노드를 차례로 방문하여, 최단경로를 찾는데 사용된다.
시작노드로부터 인접한 노드를 탐색하면서, 깊게 들어가는것 이 아닌, 같은 깊이의 노드들을 모두 방문한 다음, 다음 깊이의 노드로 넘어간다.
그럼으로, 시작노드와 가까운 노드부터 방문하게 되어 최단경로를 빠르게 찾을 수 있게된다.
코드 예시
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 먼저 방문한 노드의 상하좌우를 먼저 탐색하고.
// 전부 탐색한 다음 노드로 처리하러 이동한다.
// FIFO구조.
bool visited[9];
vector<int> graph[9];
void bfs(int start) // 시작 노드를 넣어주고 시작한다.
{
queue<int> q;
q.push(start); // 시작노드 넣어줌.
// 이 시작노드는 방문처리가 된다.
visited[start] = true;
// 방문했다는 의미를 가지는 배열을 따로 만들어준다.
while (!q.empty()) {
int x = q.front();
// 가장 앞의 요소. 가장 오래된 요소. 가져옴
// 가장 처음 들어간 요소
q.pop();
// 가져온다음 빼준다.
cout << x << ' ';
for (int i = 0; i < graph[x].size(); i++)
{// 현재 순환하는 graph의 size를 탐색한다.
// 그 후, 해당 graph에 연결되어있는 노드를전부 탐색
int y = graph[x][i];
// y 에 해당 번째의 i를 박아넣는다.
if (!visited[y])
{// 만약, 해당번째의 i가 방문한적 이 없다면,
q.push(y);
// q에 push하여 넣어주고,
visited[y] = true;
// 방문록을 작성한다.
}
}
}
}
int main()
{
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
graph[2].push_back(1);
graph[2].push_back(7);
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
graph[4].push_back(3);
graph[4].push_back(5);
graph[5].push_back(3);
graph[5].push_back(4);
graph[6].push_back(7);
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
graph[8].push_back(1);
graph[8].push_back(7);
bfs(1);
return 0;
}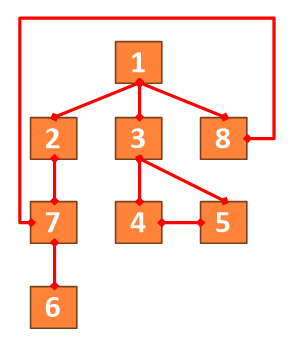
위 코드에서 1부터 가장 좌측 노드부터 탐색함으로,
1, 2, 3, 8 이 출력되고 2의 가장 가까운 7,
그이후 3의 4, 5
8은 이미 7을 탐색했음 으로 생략,
그리고 7의 6 이 출력됨으로
결과는 1238756이 나타나게 된다.
728x90
'서울게임아카데미 교육과정 6개월 C++ ~ DirectX2D' 카테고리의 다른 글
| 55일차. Queue_by_linkedlist, Tree (0) | 2023.07.10 |
|---|---|
| 54일차. Stack, Linkedlist_Stack (0) | 2023.07.06 |
| 52일차. BruteForce, Depth_first_search (0) | 2023.07.04 |
| 51일차. 충돌처리, 자료구조 - Sort (0) | 2023.06.30 |
| 50일차. XY좌표 내의 케릭터 움직임 (0) | 2023.06.29 |
