728x90
제 1 코사인법칙은, 한변의 길이와 다른두변, 그 대각 사이의 관계를 나타내는 식이다.
삼각형 ABC의 세 각을 A, B, C 라 하고, 그 대변을 각각 BC = a, AB = c, AC = b라고 할때. 다음과 같은 교환법칙이 성립한다.
a = bcosC + ccosB;
b = ccosA + acosC;
c = acosB + bcosA;
가 각각 성립한다.
a = bcosC + ccosB를 먼저 증명해보자.
선분 AH와 EC은, 각각 ccosB, ccosB와 같다.
그리고, BG와 FC를 더한값은 BC가 나타나는것을 확인할 수 있다.

나머지도 확인해보자.
b = ccosA + acosC;

b = GC + AF(뒤로갔음으로. 음수가 나옴)
c = acosB + bcosA;
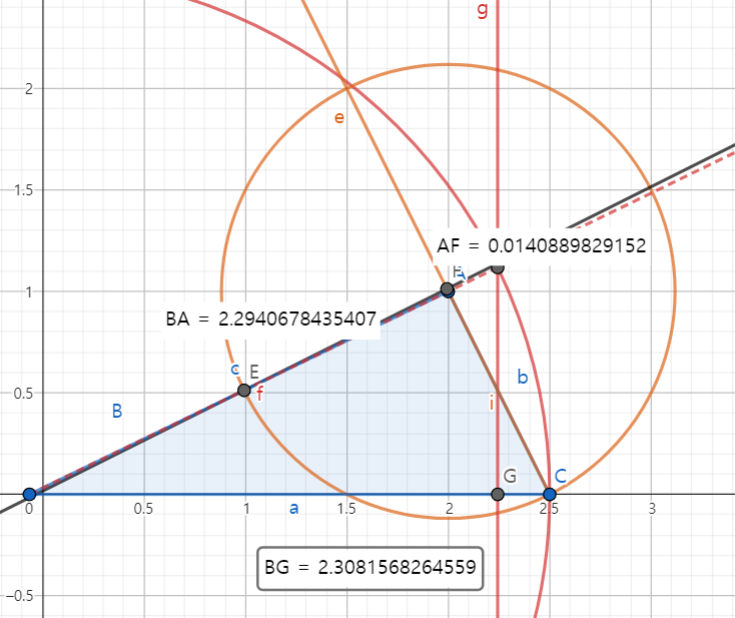
c = BA
BA = BG + AF( 뒤로갔음으로. 음수가 나옴 )
이와같이 각도와 선분에 따라 비례관계가 성립하는것이 cos 제 1법칙이다.
728x90
'컴퓨터 용어 정리 > 게임 수학' 카테고리의 다른 글
| DirectX3D 벡터의 외적 (0) | 2023.10.22 |
|---|---|
| DIrectX3D 벡터의 내적(Dot Product) (0) | 2023.10.22 |
| 삼각비 계산근거 (0) | 2023.10.21 |
| 제 2 코사인법칙 (0) | 2023.10.21 |
| DirectX 3D Vector&Scalar (0) | 2023.10.20 |
