구체 Object를 생성해보자.
정20각형을 사용해 구체 Object를 생성할 수도 있고,
아니면 원을 깎아가면서 구체를 생성할 수 있다.
두가지 다 진행해보자.
원의 둘레를 돌면서 생성하기
대부분의 사람이 알고있는 원을 그려보자.
그 원의 중심을 기준으로 선을 한개 그리게되면. 중심점을 기준으로 양분해주는 선이 생길것이다.
이걸 중심선이 아니라 옆에서 바라보았을 때의 원 한개, 위에서 바라보았을 때의 원 한개로 생각해보자.


그러면 머리속으로 그려보았을 때 대강, 십자형태로 원이 두개가 겹쳐있는 모습이 떠오를것이다.
이제 이 원 두개를 계속해서 슬라이스하면서 돌려보자.

이것이 옆에서도, 위에서도 같이 생성되었다고 하면, 구체가 체크무늬를 구성한체로 생성된다고 이해하면 된다.
그림으로 그려보았다면, 이제 수식으로 구현해보자.
각 원의 각도를 보면, 원이 이어지면서 그려지게 되려면 vertices가 임의의점 C를 찍는다고 가정하면,
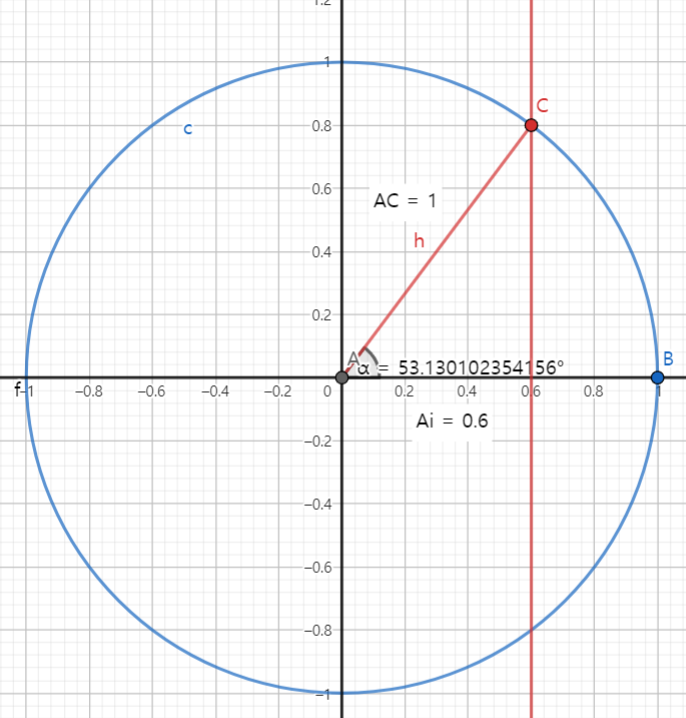
대각선의 길이는 원의 반지름임으로 항상 1로 고정이고,
C의 Y축은 sin(α) 일것이고, x축은 cos(α)일것이다.
평면상 위치는 위와 같고, z축은 깊이값임으로, 현재 vertices의 회전각에 따라 달라질것이다.
이제 vertices를 찍어보자.
float thetaStep = XM_2PI / sliceCount;
float phiStep = XM_PI / stackCount;
vector<VertexType>& vertices = mesh->GetVertices();
vertices.reserve((sliceCount + 1) * (stackCount + 1));
for (UINT i = 0; i <= stackCount; i++)
{
float phi = i * phiStep;
for (UINT j = 0; j <= sliceCount; j++)
{
float theta = j * thetaStep;
VertexType vertex;
vertex.normal.x = sin(phi) * cos(theta);
vertex.normal.y = cos(phi);
vertex.normal.z = sin(phi) * sin(theta);
vertex.pos = Vector3(vertex.normal) * radius;
vertex.uv.x = (float)j / sliceCount;
vertex.uv.y = (float)i / stackCount;
vertices.push_back(vertex);
}
}위 코드에서는 i와 j를 sliceCount로 계산한다.
현재 위치값의 position 을 x축기준으로 몃번 자르는지? y축 기준으로 몃번 자르는지를 정의한다.
즉, x축기준으로 32번 자른다고 하면, 180도기준으로 sin(180/32 * i) 또는 cos(180/32 * j)가 해당 범위의 위치가 될것이다.
pos값은 Vector3(vertex.normal)에 radius (원의 반지름) 을 곱하여 position이 갱신된다.
uv값은, 현재 uv위치값이 0.0부터 1.1로 수렴함으로 i / sliceCount를 하여. 32분할로 한 값을 기입해주면 된다.
vertices를 찍었으면, indices를 찍어야 한다.
vector<UINT>& indices = mesh->GetIndices();
indices.reserve(sliceCount * stackCount * 6);
for (UINT i = 0; i < stackCount; i++) {
for (UINT j = 0; j < sliceCount; j++) {
indices.push_back((sliceCount + 1) * i + j); // 0
indices.push_back((sliceCount + 1) * i + j + 1); // 2
indices.push_back((sliceCount + 1) * (i + 1) + j); // 1
indices.push_back((sliceCount + 1) * (i + 1) + j); // 1
indices.push_back((sliceCount + 1) * i + j + 1); // 2
indices.push_back((sliceCount + 1) * (i + 1) + j + 1); // 3
}
}각 vertices를 이어주는 indices순서이다.
좌표의 순서도는. 32개를 기준으로 180도를 나누었을 때. sincos를 대입한 position이 어떤식으로 찍히는지 3차원도표를 통해 확인하면 쉽게 확인할 수 있다.
0번째 vertices는 윗쪽부터 전체적으로 찍어지고, 1번째는 y축이 한번 내려간 상태에서 x축의 반지름 길이가 cos만큼으로 정해짐으로. cos값을 대입하여 반지름을 측정한뒤, y축을 sin만큼 내려서 찍어준다.
이러한 좌표를 이해하면 쉽게 indices의 순서를 유추할 수 있다.

정20각형으로 구체 만들기
정20각형으로도 구체를 생성할 수 있다.
정 다면체 중 구에 가장 가까운 다면체는 정20각형 임으로. 정20각형을 만들고 subdivision을 하게 되면,
정 다면체가 균힐하게 쪼개지면서 점점 구체에 가까워질것 이다.
다음과 같은 Verteics를 구성해볼 수 있을것이다.
// 정 20면체의 각 삼각형 길이 황금비.
double X = 0.525731f;
double Z = 0.850651f;
vector<VertexType>& vertices = mesh->GetVertices();
vertices.emplace_back(-X, 0.0f, +Z, 0, 0);
vertices.emplace_back(+X, 0.0f, +Z, 1, 1);
vertices.emplace_back(-X, 0.0f, -Z, 0, 0);
vertices.emplace_back(+X, 0.0f, -Z, 1, 0);
vertices.emplace_back(0.0f, +Z, +X, 0, 1);
vertices.emplace_back(0.0f, +Z, -X, 1, 1);
vertices.emplace_back(0.0f, -Z, +X, 0, 0);
vertices.emplace_back(0.0f, -Z, -X, 1, 0);
vertices.emplace_back(+Z, +X, 0.0f, 0, 1);
vertices.emplace_back(-Z, +X, 0.0f, 1, 1);
vertices.emplace_back(+Z, -X, 0.0f, 0, 0);
vertices.emplace_back(-Z, -X, 0.0f, 1, 0);
vector<UINT>& indices = mesh->GetIndices();
//각 꼭짓점을 삼각형 형태로 이어서 긋는 순서를 시계방향으로 배치.
indices =
{
1,4,0,
4,9,0,
4,5,9,
8,5,4,
1,8,4,
1,10,8,
10,3,8,
8,3,5,
3,2,5,
3,7,2,
3,10,7,
10,6,7,
6,11,7,
6,0,11,
6,1,0,
10,1,6,
11,0,9,
2,11,9,
5,2,9,
11,2,7
};각 vertices가 구를 생성할 때, 반지름이 1일경우, 정20면체의 각 vertices의 위치값은 X와 Z의 각 값으로 정할 수 있다.
위 순서대로 정20면체의 vertices를 그릴 수 있다.
// Save a copy of the input geometry.
vector<VertexType> verticesCopy;
vector<VertexType>& nowVertex = mesh->GetVertices();
for (const auto& def : nowVertex)
verticesCopy.push_back(def);
vector<UINT> indicesCopy;
vector<UINT>& nowIndices = mesh->GetIndices();
for (auto def : nowIndices)
indicesCopy.push_back(def);
nowVertex.resize(0);
nowIndices.resize(0);
// v1
// *
// / \
// / \
// m0*-----*m1
// / \ / \
// / \ / \
// *-----*-----*
// v0 m2 v2
UINT numTris = indicesCopy.size() / 3;
for (UINT i = 0; i < numTris; ++i)
{
VertexType v0 = verticesCopy[indicesCopy[i * 3 + 0]];
VertexType v1 = verticesCopy[indicesCopy[i * 3 + 1]];
VertexType v2 = verticesCopy[indicesCopy[i * 3 + 2]];
//
// Generate the midpoints.
//
VertexType m0 = MidPoint(v0, v1);
VertexType m1 = MidPoint(v1, v2);
VertexType m2 = MidPoint(v0, v2);
//
// Add new geometry.
//
nowVertex.push_back(v0); // 0
nowVertex.push_back(v1); // 1
nowVertex.push_back(v2); // 2
nowVertex.push_back(m0); // 3
nowVertex.push_back(m1); // 4
nowVertex.push_back(m2); // 5
nowIndices.push_back(i * 6 + 0);
nowIndices.push_back(i * 6 + 3);
nowIndices.push_back(i * 6 + 5);
nowIndices.push_back(i * 6 + 3);
nowIndices.push_back(i * 6 + 4);
nowIndices.push_back(i * 6 + 5);
nowIndices.push_back(i * 6 + 5);
nowIndices.push_back(i * 6 + 4);
nowIndices.push_back(i * 6 + 2);
nowIndices.push_back(i * 6 + 3);
nowIndices.push_back(i * 6 + 1);
nowIndices.push_back(i * 6 + 4);
}그 후에 위 코드를 살펴보면 Subdivide에 대한 정보를 알 수 있다.
indices가 이어지는 순서대로 vertices를 잡고. 해당 vertices대로 중점을 찍은다음,
해당 중점을 기준으로 다시 indices를 이어주면 쉽게 분할이 가능하다.
XMVECTOR p0 = XMLoadFloat3(&v0.pos);
XMVECTOR p1 = XMLoadFloat3(&v1.pos);
XMVECTOR c0 = XMLoadFloat2(&v0.uv);
XMVECTOR c1 = XMLoadFloat2(&v1.uv);
XMVECTOR e0 = XMLoadFloat3(&v0.normal);
XMVECTOR e1 = XMLoadFloat3(&v1.normal);
// Compute the midpoints of all the attributes. Vectors need to be normalized
// since linear interpolating can make them not unit length.
XMVECTOR pos = 0.5f * (p0 + p1);
XMVECTOR uv = XMVector2Normalize(0.5f * (c0 + c1));
XMVECTOR normal = XMVector3Normalize(e0 + e1);
VertexType v;
XMStoreFloat3(&v.pos, pos);
XMStoreFloat2(&v.uv, uv);
XMStoreFloat3(&v.normal, normal);
return v;위 코드는 중점을 찾아주는 코드이다.
vertices의 중점을 찍어주는 역할을 한다.
만약 다른 중점의 위치가 필요하다면 해당 중점 위치를 찍어줄 수 있을것이다 (예를들면 NormalizeMap같은 경우 해당 좌표를 찍어야할것이다)
for (auto& vertex : vertices)
{
float theta = atan2(vertex.pos.z, vertex.pos.x);
float phi = acos(vertex.pos.y / size);
float u = theta / (2.0f * XM_PI);
float v = phi / XM_PI;
vertex.uv.x = v;
vertex.uv.y = u;
}위 코드는 해당 구체의 vertices의 위치값을 참조하여 2DUVmap에 투영하는 코드이다.
그러나, 구체UV맵을 수정하지 않으면 UV값의 끝부분의 차이로 인해 선분이 나타날 수 있다.

노말맵 & 스펙큘러 적용하기
지금까지 적용했던 빛은, 정반사와 난반사이다.
이러한 정반사와 난반사는 빛의 번짐이 어떤식으로 적용되는가를 사용하기위해
난반사는 Object와 발광체 를 가지고 법선데이터를 활용하여 연산을 하였고,.
정반사는 Object 와 발광체, 카메라의 position을 가져와서 연산을 하였다.
스펙큘러 맵은, 빛의 반사광을 다루는 맵중에 매우 단순한 방법을 사용한다.
스펙큘러맵

위 이미지가 스펙큘러 맵이다.
아주 간단하게 Light의 정도를 조절해주는데,
검정색이면 LIght의 빛반사정도를 0으로, 옅을수록 1에 가깝게 바꿔주는 매우 단순한 방식이다.
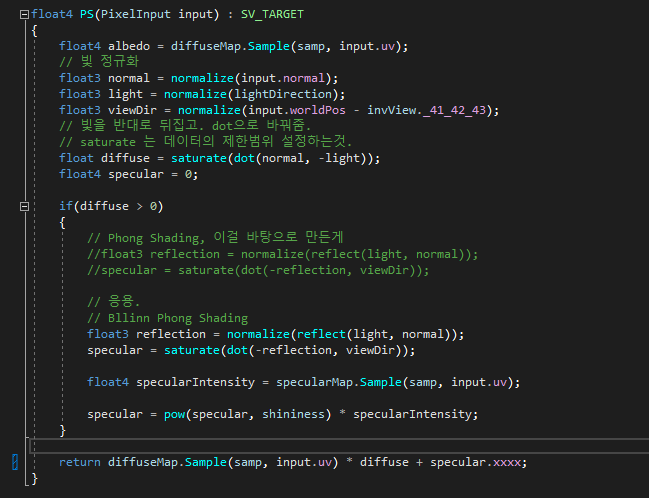
스펙큘러맵을 적용하는 hlsl이다.
class Material
{
public:
Material(wstring shderFIle);
~Material();
void Set();
void SetShader(wstring shaderFile);
void SetDiffuseMap(wstring textureFile);
void SetSpecularMap(wstring textureFile);
void SetNormalMap(wstring textureFile);
private:
VertexShader* vertexShader;
PixelShader* pixelShader;
Texture* normalMap = nullptr;
Texture* diffuseMap = nullptr;
Texture* specularMap = nullptr;
};데이터는 언제나 그렇듯 Material에서 관리하여 가져와 사용한다.
정반사의 hlsl에 스펙큘러 맵을 적용한 모습니다.
specularMap을 Texture로 받아온다음, 현재 uv위치에 Sample하여. color값을 받아온 다음, x값만 데이터를 더해주면된다.
specular에 pow를 해주는 것은, 정반사의 정도를 제곱해주어 정반사의 빛번짐값을 같이 가져올 수 있도록 해준다.

스펙큘러맵을 적용한 이미지.
검정색 부분인 벽돌의 흙부분이 빛번짐이 이루어지지 않음을 확인할 수 있다.
노말맵
이친구가 제일 골때리는 친구인데,
노말맵이란,
현재 우리가 사용하는 법선 데이터는. Vertex의 V2 - V0, V1 - V0 값을 사용하여 면에서부터 나타나는 법선을 사용한다.
이러한 법선 데이터는 일정하게 면에서 수직되게 표현되는데.
이런 데이터로는 스펙큘러 맵에서 보는것과 같이. 평면적이게 맵이 표현된다.
하지만, 게임에서 보면 대부분의 RACE는 굴곡이 있는것처럼 보이게 표현된것을 알 수 있는데.
이러한 굴곡을 표시하기 위해 사용하는것이 노말맵이다.

이 이미지는 노말맵 이미지이다.
이 노말맵을 사용해서 굴곡을 나타내는데,
쉽게 생각하면 우리가 도장을 파내서 만들듯, 벽에 부드러운 찰흙을 붙인뒤 바로 떨어뜨리면 나타나는 벽모양이라고
생각하면 된다.
각각 RGB데이터가 X,Y,Z축에 대한 법선데이터의 방향을 나타내는데.
각 법선데이터에 위 노말맵을 더한뒤 Normalize해주면. 방향이 수정된 법선이 나타나게 된다.
그러나, 가장 큰 문제가 하나 있는데. 각도가 수정되는 법선 데이터의 기준을 알 수 있는 방법이 매우 재한적 이라는것이다.
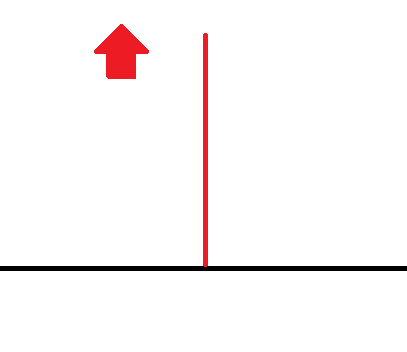
위와같이 법선데이터가 나타나있다고 생각해보자. 우리는 여기서 알 수 있는 데이터는 법선데이터의 위 가 어디인지 밖에 없다.
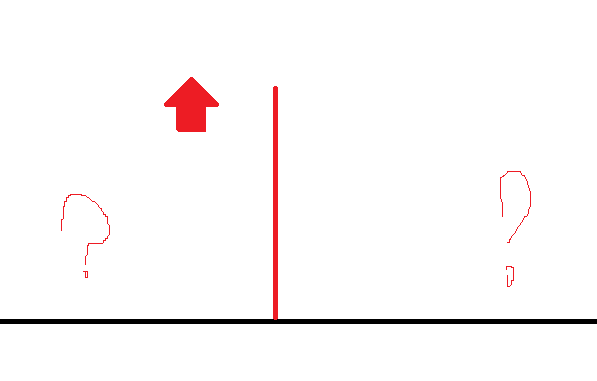
그저 위 방향이 법선의 진행방향이라는것만 알고있지. 어디가 좌측인지 어디가 우측인지 어디를 X축으로 Z축으로 해야하는지 모른다.
이런 골때리는 문제를 해결하기 위해 우리는 UV데이터를 사용하여 노말맵의 X축 Y축을, 현재 맵핑된 Object의 UV상 X축, Y축을 결정해야한다.
법선, 노말맵의 X축Y축 결정하기
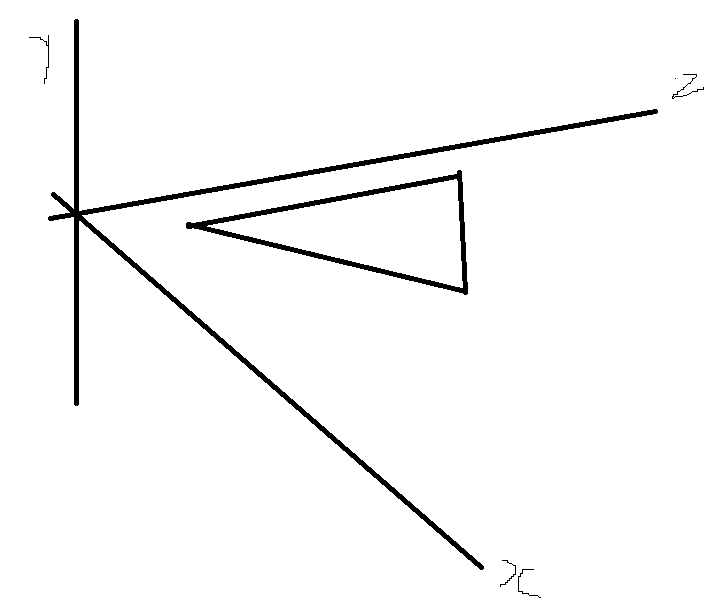
위 이미지와 같은 UV맵이 존재한다고 해보자.
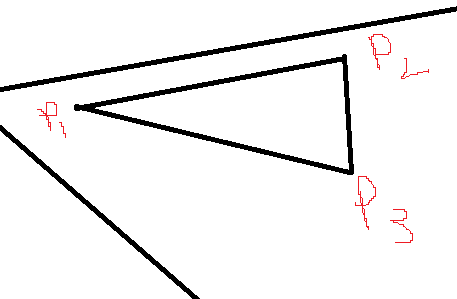
위와같은 포인트로 지정하고 생각해보면, UV맵상의 법선을 그려야 할것이다.
이건 우리가 법선을 만들어낼 때 사용한 방법을 그대로 사용하게 되는데.
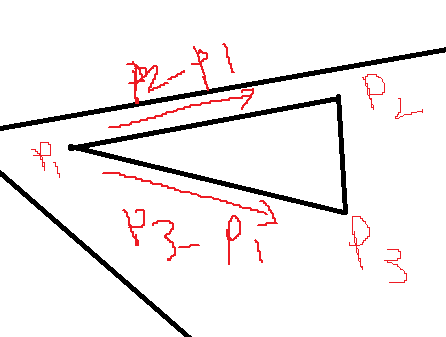
위 이미지와 같은 벡터간 뺄샘을 사용해서 해당 방향으로 이동하는 벡터를 구할 수 있는데.

대강 위와같이 정리될것이다.
여기에서, 현재 UV값의
N방향은 world상의 법선데이터
T방향을 구하는게 조금 힘들다.
위 P1->P2 와 P1->P3를 구하는 공식을 살펴보면 다음과 같다.고 할 수 있는데,
먼저 이해를 돕기위해 다음과 같이 사용해보자.
P1->P2의 xy축은 각각(v0, v1)이라고 하고, P1->P2 는 e0
P1->P3의 xy축은 각각(u0, u1)이라고 하고, P1->P3 는 e1
이라고 할 때.
T x u0 + B x v0 = e0
T x u1 + B x v1 = e1
이라고 할 수 있고.
이를 행렬로 표현하면.
(u0v0u1v1)(TB)
와 같이 나타나는데,
여기서 우리는 T와 B값을 구하기위해 어떤걸 해야하는가?
(u0v0u1v1)
의 역행렬을 곱해버리면 된다.
D=u0×v1−v0×v1
여기서 역행렬은 위와 같다.
이제 이 수식들을 코드로 표현해보자.
vector<VertexType>& vertices = mesh->GetVertices();
vector<UINT>& indices = mesh->GetIndices();
FOR(indices.size() / 3)
{
UINT index0 = indices[i * 3 + 0];
UINT index1 = indices[i * 3 + 1];
UINT index2 = indices[i * 3 + 2];
Vector3 p0 = vertices[index0].pos;
Vector3 p1 = vertices[index1].pos;
Vector3 p2 = vertices[index2].pos;
Float2 uv0 = vertices[index0].uv;
Float2 uv1 = vertices[index1].uv;
Float2 uv2 = vertices[index2].uv;
Vector3 e0 = p1 - p0;
Vector3 e1 = p2 - p0;
float u0 = uv1.x - uv0.x;
float v0 = uv1.y - uv0.y;
float u1 = uv2.x - uv0.x;
float v1 = uv2.y - uv0.y;
float d = 1.0f / (u0 * v1 - v0 * u1);
Vector3 tangent = d * (e0 * v1 - e1 * v0);
vertices[index0].tangent += tangent;
vertices[index1].tangent += tangent;
vertices[index2].tangent += tangent;
}T방향의 값은 d가 역벡터임으로. 벡터값에 d를곱하면 t방향의 값이 나타난다.
B는 거기서 90도 돌리면된다.
PixelInput VS(VertexUVNormalTangent input)
{
PixelInput output;
output.pos = mul(input.pos, world);
output.worldPos = output.pos;
output.pos = mul(output.pos, view);
output.pos = mul(output.pos, projection);
output.uv = input.uv;
output.normal = mul(input.normal, (float3x3) world);
output.tangent = mul(input.tangent, (float3x3) world);
output.binormal = cross(output.normal, output.tangent);
return output;
}
float4 PS(PixelInput input) : SV_TARGET
{
float4 albedo = diffuseMap.Sample(samp, input.uv);
float3 T = normalize(input.tangent);
float3 B = normalize(input.binormal);
float3 N = normalize(input.normal);
// 빛 정규화 작업.
float3 normal = N;
float3 light = normalize(lightDirection);
float3 viewDir = normalize(input.worldPos - invView._41_42_43);
float3 normalMapColor = normalMap.Sample(samp, input.uv).rgb;
normal = normalMapColor * 2.0f - 1.0f; // 0~1 -> -1~1
float3x3 TBN = float3x3(T, B, N);
normal = normalize(mul(normal, TBN));
// 빛을 반대로 뒤집고. dot으로 바꿔줌.
// saturate 는 데이터의 제한범위 설정하는것.
float diffsue = saturate(dot(normal, -light));
float4 specular = 0;
if (diffsue > 0)
{
//Blinn Phong Shading
float3 halfWay = normalize(viewDir + light);
specular = saturate(dot(normal, -halfWay));
float4 specularIntensity = specularMap.Sample(samp, input.uv);
specular = pow(specular, shininess) * specularIntensity;
}
float4 ambient = albedo * 0.1f;
return diffuseMap.Sample(samp, input.uv) * diffsue + specular + ambient;
}
위에서 구한 uv상 벡터를 사용해서. TBN값을 설정할 수 있다.
n은 법선,
T는 구했던 역벡터를 곱한값.
B는 tangent에 normal을 외적해버리면 된다.
결과로는. 그대로 사용하는 데이터에 diffsue가 수정된 법선데이터 에 light를 cos한 값임으로 곱해주면된다.


'서울게임아카데미 교육과정 6개월 국비과정' 카테고리의 다른 글
| 20231026 17일차 머티리얼조정, 세이브로드 (0) | 2023.10.26 |
|---|---|
| 20231025 16일차 라이팅맵 조정, 라이브러리 정리 (0) | 2023.10.25 |
| 20231020 13일차 카메라 움직임 구현, 라이팅구현1 (0) | 2023.10.22 |
| 20231019 12일차 Plore 만들기, View State설정 (0) | 2023.10.19 |
| 20231018 11일차 프레임워크 통합(srv, ImGui 추가) (0) | 2023.10.18 |
